n次元多様体のロマン
ルネ・マグリットの「白紙委任状」という絵はご存知でしょうか。「馬に乗った女性が木々の間を通過しつつ木々を隠している絵」と言えば思い出される方も多いと思います。この見る者を戸惑わせる絵は「私たちの住む3次元空間では実現できない」と言われることがありますが、では仮に私たちが高次元の空間に住んでいて、例えば5番目の次元を利用できるなら実現が可能なのか…。
大学などの高等教育の数学分野では、目に見えない次元にある図形について考える「位相幾何学」を真摯に探究する研究者がいらっしゃいます。「3次元空間に実現できない高次元の図形」なる言葉に惹かれ、信州大学理学部数学科の境圭一准教授にお話を伺ってきました。（文・柳澤 愛由）
PROFILE：境 圭一 准教授
信州大学学術研究院（理学系）准教授
理学部数学科数理科学コース（幾何学分野）
2007年 東京大学大学院数理科学研究科博士課程修了（数理科学）
2010年 日本学術振興会特別研究員（信州大学理学部赴任）
2011年 信州大学理学部助教
2016年 信州大学学術研究院（理学系）准教授、現在に至る
・・・・・ 信州大学広報誌「信大NOW」第122号（2020.3.31発行）より
すでに解決した、という「ポアンカレ予想」からみる位相幾何学の奥深さ
多くの数学者が挑んできた「ポアンカレ（Poincare）予想」をG.Perelmanという数学者が解決したと発表したのは、2002年から2003年のことでした。1904年にフランスの数学者アンリ・ポアンカレによって提出されて以来、実に100年近くの時間を要したことになります。
ポアンカレ予想における問題とは、「単連結な3次元閉多様体は3次元球面と同相といえるか？」というものでした。数学的に厳密ではありませんが、例えば、「長いロープを結んだロケットが、任意の点から宇宙を一周して戻ってきたとします。ロケットがどのような軌道を描いたとしてもロープの両端を引っ張ってロープを全て回収できた場合、宇宙の形は概ね球体（＝ドーナツ型のような穴のある形、ではない）と言えるのか」という問題です。これが、「位相幾何学の究明が宇宙の形を知ることにつながる」所以です。
境圭一准教授は、空間や次元の概念を通じて、図形の性質や姿を見て、分類したり、明らかにしたりする「幾何学的トポロジー」と呼ばれる分野が専門です。例えば、私たちが絵に描けるのは2次元まで。3次元空間における図形は、厳密には絵に描くことはできません。4次元、5次元とさらに高次元になっていけば、よりその姿を「見る」ことが難解になっていきます。
物理学の世界では、我々がいる時空を「空間3次元・時間1次元」の4次元と捉えることがありますが、「位相幾何学」においては次元軸を定義づけることはしません。4次元空間は、ある一定の方向に伸びた座標軸が4つあるということ。さらに言えば、4つの実数の組全体がなす集合です。数式に表せば次のようなものになります。
R⁴ =｛(x1,x2,x3,x4)｜xi は実数｝
数式であればシンプルに表せても、今我々が生きている次元では描けないものを探求する…なんとも不思議な感覚になりますが、考え方を変えればちょっとロマンのある話ではないでしょうか。
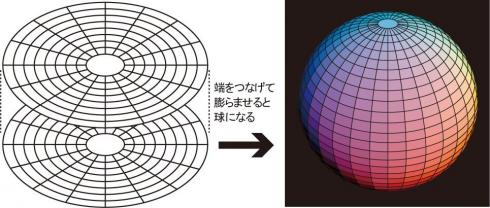
2次元で作った球面で知る多様体の「埋め込み」という理論・概念
同じ大きさの円形を2つ作り、ふちに沿って貼り合せ膨らませていくと（少しシワが寄る感じがするが）球体になっていく。平面的な2次元の図形が3次元空間に出現した“埋め込み”の一例である。我々が今立つ地球の一部は平面だが、本当は球体に立っており、図形というものを通じて「本当の姿を見る・知る」ことができる。
境准教授が研究テーマとするのが、「埋め込み」という理論。ある次元にある多様体を、もっと高い次元の空間内に実現することで、図形を「見る」ための手段のひとつです。
「地球の表面だけを見て中身を考えなければ、地球は2次元球です。その2次元球の上に住んでいる私たちが、『地球は丸い』ことを知るためには、地球から離れて実際に見るのが手っ取り早い。より高次元である3次元空間（宇宙空間）に2次元球の地球が入っている＝埋め込まれていることで、私たちは地球が球であることを見ることができるのです」（境准教授）
「埋め込み」について、もう少し詳しくお聞きしました。
「例えば、円形の紙（２次元）を２枚用意して、ふちに沿ってテープで張り合わせ膨らませると少ししわの寄った球になりますよね。これは平面的な紙（2次元の図形）でつくった『球面』という2次元図形が、私たちの住む3次元空間へ現れたことになります。これが2次元の3次元空間への『埋め込み』の一例です」（境准教授）
位相幾何学で解明したものが、すぐに私たちの実生活につながる何かを教えてくれる訳ではありません。しかし位相幾何学で導き出された論理は、宇宙論や素粒子論、近年では「位相的データ解析」といったビックデータの解析にも、盛んに使われています。
「応用なんて考えずにやっていた研究が、実は役に立っていることもある。多くの数学者は実生活に直結するか否かで物事の価値を測ってはいけないと考えています」（境准教授）
「埋め込み」の説明に欠かせないのが、「絡み目」という考え方です。私たちが生きているのは3次元空間なので、3次元における図形のことは良く分かりそうなものですが、実は「3次元や4次元といった低い次元が一番難しい」と境准教授。それも「絡み目」の問題に集約されるそうです。
「埋め込み」に欠かせないのが「絡み目」。絡まり方は様々だが、例えば左はX・Y・Z軸でそれぞれの2つの軸（2次元）に描いた円を交差した例。2つの輪を見れば交差していないが、もうひとつの軸の輪と絡み合って解けない。なんとも単純に見えるが実は深く、3次元の図形の分類は、このような絡み目の分類とほぼ等価であるらしい。
例えば、1つの輪っか（円周）が絡まったものが、位相幾何学でいう「絡み目」です。輪っか（円周）＝1次元球面なので、それが
「絡まった状態」というのは、1次元球面の3次元空間への「埋め込み」にほかなりません。輪っかの絡まり方は無限にあり、多種多様です。それが3次元における問題の難しさにつながっているといいます。そのほか、境准教授が「埋め込み」の分かりやすい例として紹介してくれたのが「ボロミアン環」（右図）。ボロミアン環は、2つの輪っかだけであれば分離可能であるのに、3つの輪っかが「絡まる」ことで、分離不可能な状態になった図形です。
「さまざまな形で埋め込まれた図形を、何らかの方法で分類することが、位相幾何学における非常に重要な研究テーマのひとつです。例えば、交差をひとつ変えることで、『解ける』絡み目になることもあれば、『解けない』絡み目になることもある。実はそれが、タンパク質と酵素の働きの解明につながることもあるそうです」（境准教授）
「埋め込み」の研究の中でも、境准教授が専門としているのが「多様体（図形）を1つ決めて、その図形における多種多様な埋め込みを全て一斉に考え、その様相を調べること」だといいます。とくに境准教授は、5次元、6次元といった高次元での問題に興味を惹かれているそうです。
「例えば、さまざまな埋め込み方をした1つの図形を一斉に集めます。そうしてできた『結び目の集合体』は、また新しい図形になり、幾何学的対象になるんです。その新しい図形は抽象的なもので目には見えないのですが、例えば、その図形に『穴』がある、ということを見つける方法があるはずなんです。そんな究明を続けています」（境准教授）
「なぜ？は未来を創る原動力」子供たちや学生に知的好奇心と学びの楽しさを提供
理学の研究領域は知的好奇心の探求の場でもあります。
「この図形は学生が作ったものなんです。この図形が美しいのは、対称性が高いから。これを例えばこの方向から見て各頂点の点を結ぶと、正十二面体を形作っていることが分かります。ほかにも色々な対称性があると思います」。「三角錐を5つ組み合わせた多面体」を手にし、境准教授はそう教えてくれました。
「『青少年のための科学の祭典2019』（※）で、こういった多面体を作るブースを学生が出したのですが、親子連れには好評でした。途中から親御さんのほうが真剣になるようですが（笑）」（境准教授）
究明されていないことだらけの位相幾何学の世界ですが、「難しいからこそ面白い」と境准教授。「目には見えない図形が感覚的にわかった瞬間が一番楽しいと思います。図形を見て『おもしろそうだ』と思う気持ちを、大事にしたいですね」（境准教授）。
「なぜ？」から生まれる学びの楽しさは未来に向けた原動力だと、境准教授は微笑んでおられました。
※信州大学理学部主催の一般向けのイベント。学生が出展した理科や数学に関するさまざまな実験や展示ブースで大学研究の一端を伝えることを目的にしている
