Research Topics
-

- Collaborate
- Global
- Research
Institute for Aqua Regeneration and Faculty of Science and Technology, Thammasat University Sign Memorandum of Understanding
-

- Collaborate
- Global
- Research
Institute for Aqua Regeneration and Thai, VISTEC signed MoU
-

- Collaborate
- Global
- Research
Institute for Aqua Regeneration and Faculty of Engineering, KMUTT Sign Memorandum of Understanding
-
- Research
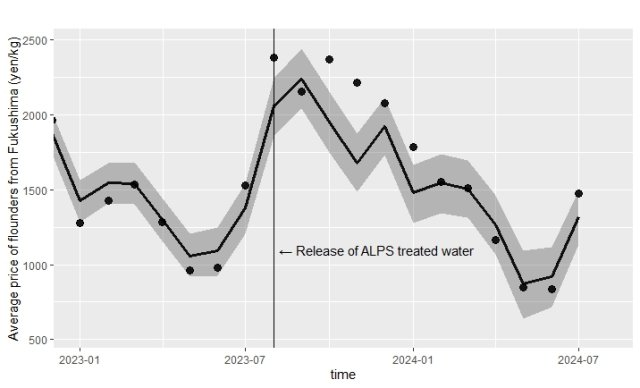
Shinshu University Finds No Price Drop in Fukushima Flounder After Treated-Water Discharge
-
- Research
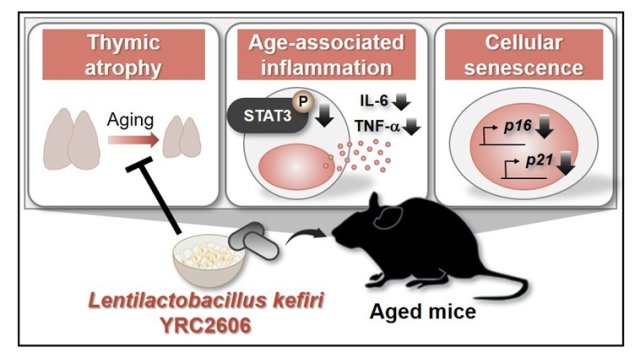
Can Certain Bacteria Regulate Aging of the Immune System and Its Related Alterations?
-

- Research
Probiotics and Prebiotics Offer Safer Alternatives to Antibiotics in Animal Agriculture
-

- Global
- Outreach
- Research
Global Spotlight on Shinshu University's Water Purifying Technology: "Shindai Crystal®" Featured in Japanese Government Video
-

- Research
Could Cardamom Seeds be a Potential Source of Antiviral Treatment?
-

- Outreach
- Research
Proposing the Future of Water and Energy at the Science Summit 2025 Held Alongside the UN General Assembly
-
- Research
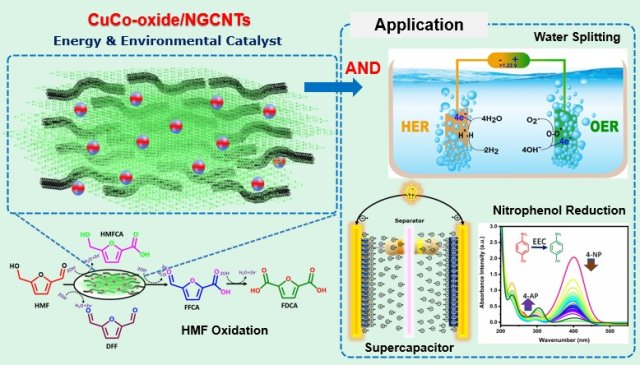
Inexpensive Multifunctional Composite Paves the Way to a Circular Economy
-
- Research
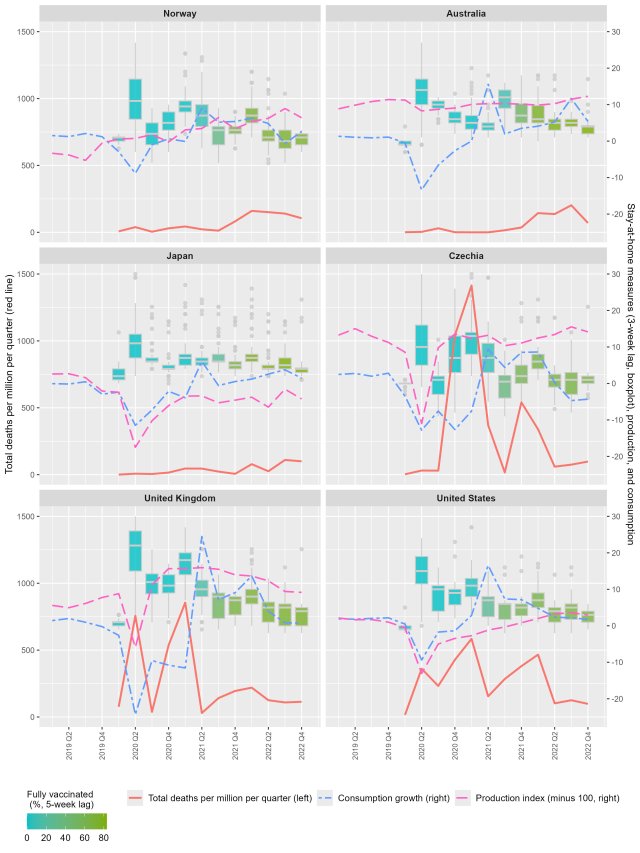
How Nations Balanced Health and Economy in the COVID-19 Pandemic: A Global Review
-
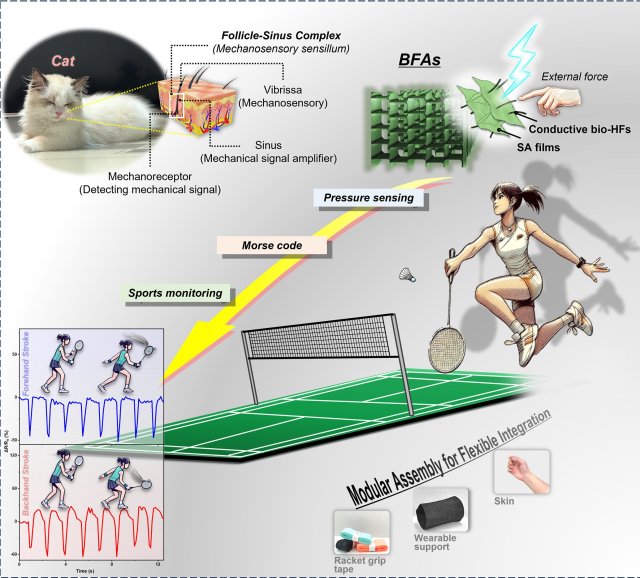
- Research
Highly Sensitive, Next-Generation Wearable Pressure Sensors Inspired by Cat Whiskers
-

- Outreach
- Research
Shinshu University Exhibits at TICAD Business EXPO Sharing Research Achievements to Co-Create the Future of Water and Energy
-

- Outreach
- Research
Shinshu University's Exhibition at the Osaka-Kansai Expo "Science: Connecting You to the Future" Event
-

- Research
Reinventing Fiber-Based Pressure Sensors

