【Research Highlight】Romance of the n-dimensional manifold
- Share
- Tweet
- Send to email
Do you know the painting “The Blank Signature” by René Magritte? Memories may be triggered by an image of a woman riding a horse behind and through trees by an optical illusion. It is said that this picture that confuse and makes viewers feel uneasy cannot happen in the three-dimensional space in which we experience everyday life, but how about in other dimensions of space such as the fifth dimension?
There are researchers who explore topological geometry which investigates figures in unseen dimensions in the field of mathematics.
Mesmorized by the phrase "high-dimensional figures that cannot be realized in 3D space" Ayu Yanagisawa spoke to Associate Professor Keiichi Sakai of the Department of Mathematics, Faculty of Science, Shinshu University.
PROFILE: Associate Professor Keiichi Sakai
Faculty of Science, Shinshu University
Faculty of Science, Department of Mathematics (Geometry)
2007 Completed doctoral course at Graduate School of Mathematical Sciences, University of Tokyo (Mathematical Science)
2010 JSPS Research Fellow (Shinshu University Faculty of Science)
2011 Assistant Professor, Faculty of Science, Shinshu University
2016 Associate Professor, Faculty of Science, Shinshu University
... First published in"Shindai NOW" No. 122 (Published March 31, 2020) Shinshu University’s public relations magazine
Exploring topological geometry from the "Poincaré conjecture"
Between the years 2002 and 2003, Russian mathematician Grigori Perelman announced he had solved the Poincaré conjecture which many before him had attempted since 1904 when the French mathematician Henri Poincaré first presented the conjecture.
The issue in Poincaré’s conjecture was whether every single connected closed 3-manifold is homeomorphic to the 3-sphere. One way in which to understand this problem, though it is not mathematically precise is to imagine a rocket with a long rope wraps around the universe from any point and pulls both ends of the rope, the shape of the rope no matter what trajectory it draws is that the shape of the universe, which is concluded to be a sphere and not a shape with a hole like a donut. This is the reason why “the study of topological geometry leads to the knowledge of the shape of the universe”.
Associate Professor Keiichi Sakai specializes in a field called geometrical topology that reveals and classifies the characteristics and shapes of figures through the concept of space and dimensions. For example, we can draw up to two-dimensions on paper. Strictly speaking, figures in three-dimensions cannot be drawn on paper. The higher the dimension becomes, for example in the fourth and fifth dimensions the more difficult it becomes to "see" it.
We sometimes think of the world we are in four dimensions, how physics defines space-time as "three dimensions of space and one dimension in time” but dimension axes are not defined in topological geometry. A four-dimensional space has four coordinate axes that extend in a certain direction. Furthermore, it is a set of all four real numbers. This can be expressed by the following mathematical formula:
R⁴ = {(x1,x2,x3,x4)|xi is a real number}
Although it can be expressed simply with a mathematical formula, exploring things that we cannot draw in the dimension we are living in feels strange. However, if we change our thinking a little, the idea might seem a bit romantic.
Theory and concept of embedding of a manifold known from a two-dimensional sphere
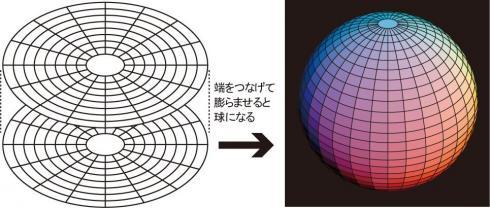
If you make two discs of the same size and stick them along the edge and inflate them (though it may seem like it is forming a wrinkle), it will become a sphere. This is an example of embedding in which a planar two-dimensional figure appears in a three-dimensional space. The part of the earth on which we stand now seems like a plane but is actually a sphere. We can see and understand this “true form” through figures.
Associate Professor Sakai's research investigates the theory of embedding. It is one of the means to see a figure by realizing a manifold in a certain dimension in a space of a higher dimension.
"If we don't look at the surface of the earth and consider its contents, the earth is a two-dimensional sphere. It is easiest to understand that the earth is round by seeing it from afar. Since the earth of a two-dimensional sphere is embedded in a higher dimensional cosmic space, we can observe that the earth is a sphere.” (Associate Professor Sakai)
More about embedding
"For example, if you prepare two sheets of circular paper (2D) and stick them along the edge with tape and inflate them, you will get a wrinkled sphere. This is an example of a two-dimensional embedding in the three-dimensional space in which we live. A flat piece of paper, a two-dimensional figure constructs a sphere which has appeared in the three-dimensional world. (Associate Professor Sakai)
Understanding topological geometry does not always immediately tell us something that will be useful in our everyday life. However, the logic derived from topological geometry is widely used in the analysis of big data such as cosmology, elementary particle theory, and in recent years, topological data analysis.
"Some research that I have done without thinking of application actually turned out to be useful in the world. Many mathematicians think that the value of a study should not be measured by whether they are immediately useful in real life.” (Associate Professor Sakai)
The concept of entanglement is essential for explaining embedding. We live in a 3D space, so it's easy to understand figures in 3D, but in reality, "low dimensions such as 3D and 4D are the most difficult," says Sakai. It is also concentrated on the problem of entanglement.
Entanglement is essential for embedding. There are various entanglement ways, but for example, the left is an example of intersecting circles drawn on each of the X, Y, and Z axes (two dimensions). If you look at two of the circles, they do not intersect, but they cannot be solved because they are intertwined with the other axis. It looks simple, but it is actually very complex, and it seems that the classification of three-dimensional figures is almost equivalent to the classification of such links.
For example, the one in which one circle, a ring, is entwined is the entanglement in topological geometry. The circle or ring is a 1-dimensional spherical surface, so it’s "entangled state" is nothing but the embedding of a 1-dimensional sphere into a 3-dimensional space. There are an infinite number of ways in which loops can be entwined. It is said that it is associated with the difficulty of the problem in 3 dimensions. Associate Professor Sakai introduced the “Borromean ring” (figure right) as an example of embedding that is easy to understand. A Borromean ring is a figure that is inseparable because three rings are entangled while it can be separated if there were only two rings.
"Classifying shapes embedded in various figures is one of the very important research themes in topological geometry. For example, changing one intersection creates a solvable link. In some cases, it may become an unsolvable link. In fact, it may lead to the elucidation of the functions of proteins and enzymes." (Associate Professor Sakai)
Among the embedding studies, Professor Sakai specializes in "picking one manifold (figure), considering all the various embeddings in that figure, and investigating the aspect". Associate Professor Sakai is particularly interested in problems in higher dimensions such as fifth and sixth dimensions.
"For example, we collect all the shapes with different embeddings all at once. The resulting assembly of knots is a new figure and becomes a geometrical object. It's abstract and invisible, but there must be a way to find out, for example, that there is a hole in the shape. I'm continuing with that investigation.” (Associate Professor Sakai)
"Why? is the driving force creating the future" Providing intellectual curiosity and learning fun to children and students
The research field of science is also a place for exploring intellectual curiosity.
"This figure was made by a student. The reason why this figure is so beautiful is that it has a high degree of symmetry. For example, if you look at it from this direction and connect the points of each vertex, you will form a dodecahedron. There are many other symmetries." He also had a “polyhedron that combines five triangular pyramids”.
At the “Festival of Science for Youth 2019 (*), students put up a booth where attendees could make such polyhedra that became popular with parents and children. Half way through, parents seem to become much more interested and involved than the children!" (Laughs Associate Professor Sakai)
Despite the fact that the world of topological geometry is full of things that have not been clarified, Associate Professor Sakai says, “It's interesting because it's difficult. “ I think the most fun I have are the moments when I can intuitively understand a figure that I cannot see. I want to cherish the feeling of pure curiosity when examining a figure.” (Associate Professor Sakai)
Associate Professor Sakai smiled contently that the joy of learning born from "why?" is the driving force for the future.
*A general event hosted by the Faculty of Science, Shinshu University. It aims to convey a part of university research through various experiments and exhibition booths related to science and mathematics exhibited by students.