Young diagrams
Here we consider the combinatorial objects called Young diagrams.
Let $n$ be a positive integer. Let us consider the positive integers $\lambda_1,\ldots,\lambda_l$ satisfying $\lambda_1+\lambda_2+\cdots+\lambda_l=n$. Since the summation of integers is commutative, assume that $\lambda_1\geq \lambda_2\geq \cdots\geq \lambda_l$.
We call a such sequece of poisitive intergers a partition of $n$. For example, the complete list of paritions of $5$ is the following: $5$, $4+1$, $3+2$, $3+1+1$, $2+2+1$, $2+1+1+1$, and $1+1+1+1+1$.
Let $\lambda_1+\lambda_2+\cdots+\lambda_l$ be a parition of $n$. Consider the diagram obtained from the partition in the following manner: Put $\lambda_1$ boxes in the first row, put $\lambda_2$ boxes in the second row, and so on. Each row should be left-justified. The diagram is called the Young diagram with respect to the partition $\lambda_1+\lambda_2+\cdots+\lambda_l$. For example, the Young diagram with respect to
the partition $5+3+3+1$ of $12$ is the following:

Conversely, for a given Young diagram with $n$ boxes, we can construct a parition of $n$. Hence we may regard a Young diagram with $n$ boxed as a partition of $n$.
A partion is nothing but a finite weakly-decreasing sequence of position intgers. The notion of partitions is very simple, but it sometimes plays important roles in many feilds. For example, Jordan blocks are parametrized by partitions, Irredusible representations of symmetric groups are parametrized by partitions, and so on.
Enumerative combinatorics
I am interested in the combinatorial objects which appears the representation theory, and study them from the view point of enumerative combinatorics.
A Young diagram is a diagram corresponding to a parition of an intger. We also consider the diagram with no box, which is denoted by $\varnothing$. The Yong diagram $\varnothing$ corresponds to the partition of $0$.
A box in the diagram which has no boxes directly below and to the right is called a corner in the diagram. For example, corners of the Young diagram with respect to $5+3+3+1$ are the right-most boxes in the first, third and fourth rows, i.e., the boxes with $\ast$ of

The diagram obtaing from a Young diagram by removing a corner is also a Young diagram.
We also define a cocorner as follows: Consider the Young diagram with respect to $\lambda_1+\lambda_2+\cdots+\lambda_l$. Let $i$ be an integer from $1$ to $l+1$
which does not satisy $\lambda_{i-1}=\lambda_i$. The position in the $i$-th row and in the $\lambda_i+1$-th colomun is a coconer of the Young diagram. For example, coconers of the Young diagram with respect to $5+3+3+1$ are the positions with $\ast$ of

The diagram obtaing from a Young diagram by adding a box to a cocorner is also a Young diagram.
Now we consder the following process: We obatain a Young daigram with one box by adding a box to a coconer of $\varnothing$. We obatain a Young daigram with two box by adding a box to a coconer of the Young diagram with one box. We obatain a Young daigram with three box by adding a box to a coconer of the Young diagram with two box.
We repeat this proceedure and obtain a Young diagram with $n$ boxes. Now we remove a coner of the Young diagram with $n$ boxes. We repeat removing and obtain $\varnothing$. Here we call this process a growth of Young digrams of $n$ steps. For example, the following is the complete list of growths of $3$ steps:
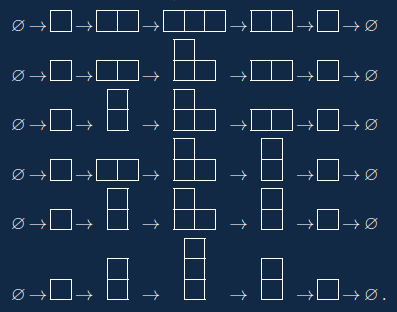
It is known that the number of growths of $n$ steps is $n!$.
Now consider another combinatorial object called a permutation. We can easily show that the number of permutations of intergers from $1$ to $n$ is $n!$: The number of candidates of the first letter of is $n$. Candidates of the second letter sould not be the same as the first letter. Hence the number of candidates of the second letter is $n-1$. Similarly, the number of candidates of the $l$-th letter is $n-l+1$. Hence the number of the permutation of $n$ letters is $n!$.
Now we have the following two equations: The number of permutation of $n$ letters is equal to $n!$. The number of growths of Young diagrams of $n$ steps is equal to $n!$.
Since the number of permutation of $n$ letters is the same as The number of growths of Young diagrams of $n$ steps, we can construct a bijection between the set of permutations and the set of growths. A bijection known as Robinson correspondence is an answer. We can translates stories of permutations to stories of growth, and vice versa. A bijection has more information than an equation.
The main subject in enumerative combinatorics is numbers of target objects. To count the number is one of purposes of our study. Moreover, if we find the equations of the number of combinatorial objects, then we also try to construct a bijection.






