Present theme: Understanding of the phase transition by using the computer simulation
The phase transition is the phenomenon in which the appearance and/or the nature of the material changes according to the change of the environment like temperature and/or pressure. For example, the water transforms from a liquid phase to a solid phase by the temperature change. The phase transition occurs when the material consists of an immense number of atoms and is characterized by the anomaly, divergence or discontinuity, of some thermodynamical quantities. In order to understand the phase transition by physics, the material is modeled as an aggregate of an immense number of particles, which mechanics is treated by either classical mechanics or quantum mechanics. The thermodynamical quantities of the modeled material are obtained by means of the prescription of statistical mechanics. The computer simulation is required to solve the equation of motion of the particles and evaluate the thermodynamical quantities from the solutions of the equation of motion. These computations are performed numerically. The key quantity of the phase transition is the free energy of the material. The anomaly of the thermodynamical quantities is ascribed to the free energy. It is considered that the magnitude correlation of the free energy of the two phases changes when the phase transition occurs. This change results in the anomaly of some thermodynamical quantities. In principle the free energy can be evaluated by statistical mechanics, but in practice it is hard to evaluate the free energy owing to the intractability of the evaluation of entropy. We perform our research to confirm the change of the magnitude correlation of the free energy for modeled material and shed the light on the mechanism of the phase transition.
brief explanation about the specialized area
Material generally has three phases, which include gas phase, liquid phase and solid phase. If, for example, a material is exposed to the environment in which the temperature, T, and the pressure, p, are fixed, the material shows one of the three phase which has the lowest free energy. In this environment the density, ρ, has the steady value. It is called the material is in the thermal equilibrium state. When the material is in the thermal equilibrium state, there is a certain relation between T, p and ρ, like p = f (T,ρ), which equation is called the equation of state. The explicit functional form of the equation of state are intrinsically determined by the material.
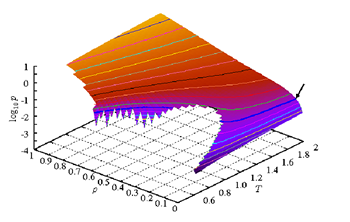
The figure shows the example of the equation of state, which is called a phase diagram. The line on the surface is an isobaric line. The isobaric line shows ρ is heightened as T is lowered. The isobaric line is disconnected at certain state points, which indicates there are two thermal equilibrium states with the same T and p but different ρ. This situation resembles to the phase transition of water, where ρ of liquid phase and solid phase is different at T = 0 ℃ and p = 1 atm. According to thermodynamics this situation is regarded as the phase transition. But the equation of state for each material can't be obtained by thermodynamics. The equation of state is in principal obtained by statistical mechanics. Statistical mechanics gives us the prescription how to obtain the free energy and the equation of state by expressing the material with proper mechanics. The free energy includes not only the mechanical energy but also the entropy, which is an important quantity for the thermodynamical properties of material. It is simply explained that the entropy indicates the randomness of the system. Suppose that ten dice are thrown. The entropy roughly corresponds to the number of cases that the sum of the spots of these dice is, for instance, 30. To evaluate the entropy, the number of cases is computed by the computer simulation.
Although the computer simulation can treat only the modeled material containing a limited number of particles, it enables to compute the thermodynamical quantities of material, which includes the entropy, from the solutions of the equation of motion. By evaluating the entropy, we can obtain the knowledge of phase transition of material as well as the phase diagram.