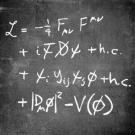Current research theme: Iterated loop spaces and their applications.
I got interested in mathematics when I read a small book "The geometry of braids" written by Kunio Murasugi. Braids are figures in the three dimensional space of the following form.
Most people are willing to unknot such entangle objects. Intuitively it is easy to understand what "unknot entangled strands" means. It is, however, not easy to describe such an operation rigorously in mathematics. If the reader is familiar with continuous maps, it is not difficult to describe this kind of "continuous deformations". But I was a high school student. It was very exciting to know that we can handle intuitive ideas such as "deformations of braids" as rigorous mathematical objects. The book told me the vast world of modern mathematics that high school students can never imagine. In particluar, I got to know that there was a very fascinating field of topology in mathematics. I decided to study topology in university.
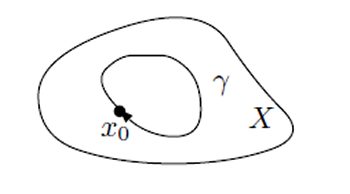
There were topologists in my university. Unfortunately, however, they specialized in more abstract field, called algebraic topology, rather than concrete geometric objects such as braids. Fortunately I found algebraic topology is also an interesting subject. In particular, I got interested in a very complicated structure, called iterated loop spaces. Given a space $X$, the loop space of $X$, denoted by $\Omega X$, is a space consisting of continuous paths in $X$ starting from a fixed point $x_{0}$ and ending at the same point $x_{0}$.
The space obtained by iterating this process $n$ times is denoted by $\Omega^{n}X$ and is called the $n$-fold loop space of $X$. It was a surprise when I learned that the case $n=2$ is closely related to braids, when I was a graduate student. This connection between braids and iterated loop spaces has been known since 1970's. My thesis advisor at the University of Rochester, Professor Fred Cohen, turned out to be one of the leading experts in this field.
Research field: Homotopy theory
Let me explain the relation between braids and iterated loop spaces in an extremely simplified way. Let $F(\mathbb{C},k)$ denote the space of $k$ distinct points in the complex plane $\mathbb{C}$. This is called the configuration space of $k$ points in $\mathbb{C}$. There is a way to construct the two-fold loop space of a sphere by gluing these configuration spaces for all $k$. And
loops in the space $F(\mathbb{C},k)$ are nothing else than braids of $k$ strands.
This configuration space $F(\mathbb{C},k)$ can be regared as the complement of hyperplanes in $\mathbb{C}^{k}$ given by $x_{i}=x_{j}$. For example
\[ F(\mathbb{C},3) = \left\{ (x_{1},x_{2},x_{3})\in\mathbb{C}^{3} \mid x_1\neq x_{2}, x_{2}\neq x_{3}, x_{3}\neq x_{1}\right\} \] is the complement of three hyperplanes $x_{1}=x_{2}$, $x_{2}=x_{3}$, and $x_{3}=x_{1}$, in $\mathbb{C}^{3}$.
Such a collection of hyperlanes is called a hyperplane arrangement and is a subject of intesive study because of the appearance in many fields. When hyperplanes are defined by equations with real coefficients, it is well known that we may construct a simplicial complex, called the Salvetti complex, in the complement. One of my recent results is a discovery of a connection between the Salvetti complex and two-fold loop spaces. I also found that, by adding hyperplanes such as $x_{1}+x_{2}=x_{3}+x_{4}$, we obtain spaces which can be used to study the global structure of the homotopy groups of spheres, which is one of the most important objectives in homotopy theory.
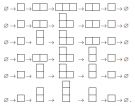
What is homotopy theory? It is one of fields in topology in which "continuous deformations", called homotopy, are the main subject of study. Among lots of new ideas developed in homotopy theory, there is a notion called operads, which play a very important role in the study of connections between braids and iterated loop spaces. In order to understand this idea, let us consider the following examples of two rivers.
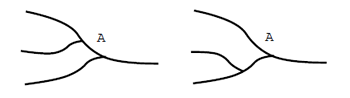
If you live in the town $A$, you with notice that these two rivers are different. When there is a heavy rain in the upstream of the middle stream, the town $A$ will have floods in the case of the left configuration. However the town $A$ will not be touched by floods in the case of the right configuration. Those who live near the mouth of the river will have floolds anyways. Their viewpoint can be nicely expressed as an equation
\[ (a\cdot b)\cdot c = a\cdot (b\cdot c). \]
On the other hand, those who live in upstreams care where streams come together. The notion of operads was introduced in order to describe intermediate stages of operations.
The reader might have noticed that we may continuously deform the left river to the right river. Operads are also closely related to such continuous deformations of operations.
In a loop space, we may concatenate two loops, which defines a "multiplication" on the loop space. This is one of the first occasion in which deformations of operations appeared. This is where the notion of operads was born. Nowadays operads are used to describe various geometric and algebraic structures. Algebraic structures appearing in mathematical physics can be also described in terms of operads.
Another important notion in homotopy theory is that of "model category", which is an abstraction of the notion of homotopy. It can be used to import "continuous deformations" in varous fields such as
- the theory of concurrency in computer science,
- noncommutative algebraic geometry,
- mathematical logic
- $\cdots$
The notion of model categories gives us a global viewpoint. One of the origins of such a viewpoint is the work of Eilenberg and Mac Lane who introduced and developed category theory. Besides "continuous deformations", this global viewpoint characterizes the field of homotopy theory.