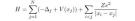現在の研究テーマ: 確率(偏)微分方程式の解の長時間の振る舞い
Newtonの力学法則にしたがう自然現象は常微分方程式によって記述されます.このような自然現象においては,ある時刻における状態がわかると, 常微分方程式を解くことによりすべての時刻における状態が完全に決定されます.
しかし現実には,このような記述の不可能な現象が数多く存在します. 例えば,1828年にイギリスの植物学者R. Brown (1773--1858) は液体中に浮遊する花粉から出てくる微粒子が極めて不規則な運動をすることを発見しました. このような運動はその典型的な例の一つです. その後,この運動は液体の分子とのランダムな衝突によることが解明され,1923年に, N. Wiener (1894--1964)はその現象を理想化し, 数学的モデルを確率過程として捉えることに成功しました. このような確率過程をBrown運動,またはWiener過程と呼びます.以下では,Brown運動を$(B_t)_{t\geq 0}$で表します.
上記のような決定論的記述ができない現象を考察するとき,ランダムな揺らぎの効果を考慮する必要が生じます.このような現象を数学的に記述するのが確率微分方程式なのです.確率微分方程式とは,大まかに言えば時間とともに偶然に変化する要因を伴った常微分方程式です.これは,1942年に伊藤清 (1915--2008)により初めて導入されたもので,今日,数学の分野に留まらず,物理学, 生物学,工学,経済学などの分野において盛んに応用されています.
さて,研究テーマを説明するために,例として,下記の簡単な二つの確率微分方程式を考えてみましょう.
\begin{align} dX(t) & = -aX(t) dt + \sigma dB(t), \ X(0)=x. (1) \\ dY(t) & =b Y(t) dt + \beta Y(t) dB(t), \ Y(0)=y. (2) \end{align}
ただし,$a, b, \sigma, \beta$は正の定数です.
確率微分方程式(1)は摩擦のある粒子の不規則な運動を記述するLangevin方程式と呼ばれます.伊藤の公式を用いれば,その解は
$$ X(t)=\exp\{-at\}x+ \int_0^t \exp\{-a(t-s)\}\sigma dB(s), \ t\geq 0 $$
であることが容易に確かめられます.また,確率過程$(X(t))_{t\geq 0}$は Ornstein-Uhlenbeck過程と呼ばれます.
確率微分方程式(2)は人口変動や株価変動を記述する重要な数学的モデルで,その解は
$$ Y(t)=y \exp \left\{(b-\frac{\beta^2}2 )t + \beta B(t) \right\}, \ t\geq 0 $$
であることが分かります.このような確率過程は幾何的Brown運動と呼ばれます.以下では,$y>0$とします.
長い時間にわたる解の振る舞いについて考えてみましょう.確率微分方程式(1)と(2)の解に対して,$t\to \infty$とすると,以下のことが知られています.
(i) $X(t)$の分布は平均$0$, 分散$\frac{\sigma^2}{2a}$の正規分布に弱収束します.
(ii) $\bullet$ $b>\frac{ \beta^2}2 $ならば,$Y(t)$はほとんど確実に$+\infty$に発散します.
$\bullet$ $b=\frac{ \beta^2}2$ならば,$Y(t)$はほとんど確実に$(0; \infty)$の間を振動します.
$\bullet$ $b<\frac{ \beta^2}2$ならば,$Y(t)$はほとんど確実に$0$に収束します.
これらの結果により,確率微分方程式(1)と(2)の見た目は似ているものの,それらの解の長時間にわたる振る舞いは完全に異なることが分かります. (i)のように,$X(t)$の分布が初期値によらず,一定の確率分布 に収束するような性質をエルゴード性といいます.また,(ii)のように,確率微分方程式の係数の取り方により,十分長い時間が経った後に,様々な挙動が起こるのは,系の安定性に関する理論により解明されます.
以上の例で分かるように,より一般な係数を持つ確率微分方程式および確率偏微分方程式(後述)に対して,長時間にわたる解の振る舞いを考察するのは,重要かつ興味深い課題となります.
研究領域: 確率偏微分方程式
私は,確率論,特に確率解析学を用いて,確率偏微分方程式に関する研究に取り組んでいます.確率偏微分方程式とは,ひとことで言えば時間および空間の変数に依存したランダムな揺らぎを持つ偏微分方程式のことです.
すでに述べたように,実際の現象を解析するためには,外部からの影響や観測の誤差などを考慮に入れる必要があります.確率偏微分方程式は,このような効果を取り組んだ上で,時間および空間に依存して変化する現象を数学的に記述する手段として用いられます. 実際,確率偏微分方程式は,物理学を始めとし,生物学,工学,経済学などの分野において現れ,種々の現象に応じて,様々な確率偏微分方程式が導入されています.例えば,弦の振動や音波の伝播を記述する確率波動方程式, %乱流のモデルとしてのランダムな外力を持つ流体の運動を記述する確率Burgers方程式や確率Navier-Stokes 方程式,超電導を記述するGinzburg-Landau方程式,揺らぎのある界面成長を記述するKardar-Parisi-Zhang 方程式などが盛んに研究されています.
私は,次のような確率偏微分方程式を主な対象として研究を行っています.
\begin{align} \frac{\partial u}{\partial t}(t, x)&= -(-\Delta)^{\frac{\alpha}{2}} u(t, x) + b(u(t,x)) \notag \\ & \qquad + \sigma(u(t,x)) \dot{W}(t,x). \label{eq-3} \end{align}
ただし,$\alpha\in (1, 2]$, $\Delta$はラプラス作用素で,係数$b$と$\sigma$はそれぞれ外力項と拡散係数 と呼ばれる関数で,$\dot{W}(t,x)$は時空ホワイトノイズを表します. 明らかに,確率偏微分方程式(3)は,確率熱伝導方程式や 合金の相分離過程を表現する確率Allen-Cahn方程式などの重要な方程式を含んでいます. このような確率偏微分方程式の解について長い時間が経過した後に,どのような様子を呈するかを調べることは重要で,とくに,解のエルゴード性,安定性,間欠性などの性質に興味をもって,研究を行ってきました.
また,高階の確率偏微分方程式にも興味を持っています.例えば,確率Cahn-Hilliard方程式
\begin{align*} \frac{\partial u}{\partial t}(t; x)&= -\Delta \big(\Delta u(t, x)+ b(u(t,x)) \big) \\ &\qquad + \sigma(u(t,x))\dot{W}(t,x) \notag \end{align*}
および反射壁を持つ確率Cahn-Hilliard方程式
\begin{align} \frac{\partial u}{\partial t}(t; x)&= -\Delta \big(\Delta u(t, x)+ b(u(t,x)) +\dot{\eta}(t,x) \big) \notag \\ &\qquad + \frac{\partial}{\partial x}\dot{W}(t,x). (4) \end{align}
です. ここで,$\eta$はランダムな測度で,外力項$b$や$u(t,x)$の値域に依存するものです. これらの確率偏微分方程式は確率Allen-Cahn方程式と同じにように合金における相分離のモデルとして採用され,重要なものです. 特に,反射壁を持つ確率Cahn-Hilliard方程式(4)は無限次元 Skorokhodの方程式と見なされ,剛体上の保存量を持つ界面モデルの平衡 揺動を記述するものであることが知られています.今後,上記のような確率偏微分方程式の長時間の挙動にも力を注ぎ,研究を進めたいと考えています.