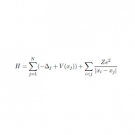Research Theme: Problems related to Kakeya conjecture
Kakeya conjecture is a big open problem in Harmonic Analysis. Here, we briefly explain this conjecture in three dimensional case. This problem was derived from a problem form Professor Soichi Kakeya (1886-1947). To understand his problem, we image a needle with the length is $1$ cm and the width is $0$ cm. His problem is whether there exists a subset of three dimensional Euclidean space, in which we can rotate the needle in every direction and the volume is $0$ or not. For example, a ball with the radius is $0.5$ cm enjoys the former property, but dose not the second one. In 1928, Besicovitch gave a result related to this problem. The subset satisfying the properties is called Kakeya set or Besicovitch set. Now, Kakeya conjecture states that Hausdorff dimension of Kakeya sets equals to the space dimension. Many mathematicians challenge to this conjecture. Although this conjecture is in the field of Geometry, we can attack Kakeya conjecture using Harmonic Analysis. One of such way is to consider the mapping properties of Kakeya maximal function:
\[ f^\ast_\delta(x) := \sup_{T \ni x} \dfrac{1}{|T|} \int_{T} |f(y)| dy, \]
Here, $T$ is a tube containing $x \in \mathbb{R}^3$ with the width is $\delta \in (0,1)$. There are other objects related to Kakeya conjecture. Among of them, the connection with wave equations:
\[ (W) \begin{cases} \; \partial_t^2 u - \Delta u = 0,\ (t,x) \in \mathbb{R} \times \mathbb{R}^n \\ \; u(0) = f,\ \partial_t u(0) = g \end{cases} \]
is the most interested one for me. The problem is so-called local smoothing conjecture.
If local smoothing conjecture is solved affirmatively, then other problems are also solved, and then Kakeya conjecture is solved affirmatively.
I am also interested in incompressible Navier-Stokes equations. I explain the equations below.
Research Area: Harmonic analysis and Partial differential equations
Harmonic analysis and Partial differential equations have the strong connection. Many researchers apply harmonic analysis to partial differential equations. Motivation of some problems in harmonic analysis come form partial differential equations.
Incompressible Navier-Stokes equations
\[ (\text{N.S.}) \begin{cases} \; \partial_t u -\Delta u + (u \cdot \nabla)u + \nabla p = 0, \\ \; \quad \quad \quad \quad \quad \quad \quad \quad (t,x) \in (0,\infty) \times \mathbb{R}^n \\ \; \mathrm{div} u = \nabla \cdot u = 0,\ (t,x) \in [0,\infty) \times \mathbb{R}^n \\ \; u(0) = a,\ (\mathrm{div}a=0), \end{cases} \]
which describe the motion of incompressible viscous fluid. Here, $u=(u_1,\ \cdots, u_n)$ is the velocity and $p$ is the pressure of the fluid, respectively. $-\Delta u$ is the friction force and $(u \cdot \nabla)u$ is the inertial force. If we consider decay property of the kinetic energy
\[ \|u(t)\|^2_{L^2} = \int_{\mathbb{R}^n} |u(t,x)|^2 dx, \]
Hardy spaces $H^p$:
\[ f \in H^p \iff f \in L^p \ \& \ \int_{\mathbb{R}^n} u(t,x) dx = 0 \]
is more useful than Lebesgue space $L^p$:
\[ f \in L^p \iff \displaystyle \int_{\mathbb{R}^n} |f(x)|^p dx < \infty. \]
(This is my opinion.) But, the definition of Hardy spaces is more difficult than that of Lebesgue spaces. One of the reasons of usefulness of Hardy spaces to Navier-Stokes equations is that the inertial force term has the cancellation property. More precisely,
\[ \int_{\mathbb{R}^n} (u\cdot \nabla)u(t,x) dx = - \int_{\mathbb{R}^n} \nabla (u \otimes u)(t,x) dx = 0. \]
Here, we used the equality $(u \cdot \nabla)u = \nabla (u \otimes u)$, which follows from the incompressible condition: $\nabla \cdot u=0$.