現在の研究テーマ:無限次元空間上の発散定理
現在までの歴史上、数学のみならず諸科学まで含めて最も大きな影響を及ぼした定理は何かといえば、おそらく間違いなく微積分の基本定理だといえると思います。微積分の基本定理とは(1 次元のときに)微分と積分がお互いに逆の演算であることを主張するものです。これは領域の内部全体での関数の値の和が、その原始関数の境界での値の差に等しいことを主張し、関数の形を適切に与えることで領域の内部における情報を外周部だけで理解できることを示しています。この事実は多次元でも一般に成り立っていることを示したのがガウスによる発散定理です。このような関係は解析学の最も基礎をなすものであり、たとえば関数概念そのものを拡張するにはいくつかの方法が知られています(総称して超関数と呼びます)が、いずれにせよ根底にはこの事実があるといってよいと思います。もちろんそれだけではなく、ベクトル解析など多くの応用の基礎となると同時に現代幾何学の基礎の一つといってもよいと思います。例えるならば、うまく関数を設置してから家の周りを一周すれば、知りたかった家の中の状況がわかるということを述べているわけです。
ところが、無限次元空間においては状況が全く異なります。最も簡単には、積分を定義するのに必要となる自然な「体積」が存在しません。たとえば体積を量るために領域を微少な(一辺1/n の)立方体を考えると、無限次元空間では最初からその値が0になってしまい、「体積要素」が考えられません。また微分ではある点とそこから少しずらした点での関数の値の差を考えることが重要ですが、このような「ずらす」ということがなかなかうまくいきません。
しかし1970 年代の末頃から、確率論のある種の研究の中でこれら両者はついに融合点を見いだし、測度論に基づいた無限次元空間上の完全な微積分の理論が完成します。この理論は通常、この方向への最初の突破口を開いた数学者の名前をとってマリアヴァン解析と呼ばれています。ところが、この理論は空間全体での部分積分の成立を示してはいますが、有限次元の場合とは異なり発散定理のような領域についてはなかなか困難がありました。有限次元の場合には有界な集合上でまず理論が作られ、むしろ空間全体へ議論を拡張するときに困難があったのとは全く対照的です。これは(ベクトルの大きさが自然に考えられる)自然な空間においては、有界閉集合がコンパクトと呼ばれるよい集合になる必要十分条件が有限次元であることであるということからくることですが、この事実が発散定理の定式化を極端に難しくします。
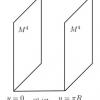
球に相当するような滑らかな領域ではすでに発散定理は定式化できていましたが、長方形のような形
に相当する角のある領域についても発散定理をマリアヴァン解析の枠組みで完全に定式化することを目指しています。
研究領域:確率解析
20 世紀初頭にアインシュタインによってブラウン運動が理論的に取り扱われると、数学的な対象としてブラウン運動を定式化することも行われました。それは[0, 1] 区間から連続関数全体が作る無限次元空間へのよい写像をフーリエ解析の手法で構成し、その空間に確率測度を導入するという方法であり、現在ではその測度はウィナー測度と呼ばれています。いったんブラウン運動という基本的な対象が数学的に定式化できると、他の拡散過程も定式化できるか、という自然な問題が起こります。ところがこれは困難であり、コルモゴロフは偏微分方程式の解に関する問題としてこれを定式化しようとしましたがあまり満足のいくところにまでは到達しませんでした。
1942 年、当時内閣統計局におられた伊藤清先生は「Markoff 過程ヲ定メル微分方程式」という革命的な論文を発表され、そこでは現在に至っても未だ神秘さを失わないブラウン運動の軌道に関する積分(伊藤積分)の方法と同時に、確率微分方程式が定義・定式化され、もしその方程式がただ1 つの解を持つならば拡散過程であることが示されていました。また、その中には後年伊藤公式と呼ばれるようになる伊藤過程を伊藤積分と通常の積分とに分解する公式もすでに現れていました。しかしこの時点では係数に滑らかさを要請せざるを得ないなどの弱点もありました。
その後解を持つための条件は1950 年代後半ころに丸山議四郎・スコロホッドらによって完全に弱められました。しかし、拡散過程の構成に関しては、田
中洋・スコロホッドによる解析的研究でも完全な解決はできませんでした。この問題は1960 年代後半にストゥルックとヴァラダンがこれら両者を統合する形で完全に解決しました。ただし伊藤の一意性と呼ばれる概念との関係は、1970 年代初頭に渡辺信三・山田俊雄らによる確率微分方程式論の完成まで待つ必要がありました。
拡散過程は実はある種の微分作用素や偏微分方程式の背後での動きを捉えている(全体の「平均」をとるとそれらが現れる)のですが、関数解析的手法でしばしば必要になる楕円性という条件が一切仮定されていません。これは大きな利点ですが、その分布や平均といった偏微分方程式の解が微分できるかどうかという問題は確率論の中では長く未解決のまま残されていました。これを解決したのが1970年代後半のマリアヴァン解析で、その理論は渡辺信三・重川一郎らによって完成され、ヘルマンダーの準楕円問題やアティヤ・シンガーの指数定理など、解析学・幾何学の重大問題に単純明快な解を与えることに成功し確率論の金字塔となりました。
ただし、確率微分方程式の解にマリアヴァン解析が適用できるのは、その解が強い解と呼ばれる場合、つまり解が雑音源から完全に再現できる場合に限られます。田中洋によって最初に発見された弱い解、つまり解のランダム性が雑音源のランダム性を上回る場合にはこのようなことができません。これら両者の違いは偏微分方程式で捉えられる構造では消えてしまうことがわかっていますが確率論としては重大な問題です。さらに、この弱い解・強い解の概念は数理ファイナンスと呼ばれる市場のモデルを構築して解析する際にも重大な問題となります。これは近年チレルソンによって導入されたノイズの概念をきっかけに、作用素環の理論などとも深い関わりを持って現在も活発に考えられている問題です。
一方現代では確率微分方程式に始まる伊藤解析、あるいはマリアヴァン解析まで込めて確率解析の数学的基礎理論はおおむね完成したと見なされており、数理ファイナンスと呼ばれる金融等に現れる問題や、厳密統計力学・場の量子論といった(これらは確率論創世期からの大きな問題意識でしたが)数理物理の諸問題が大きな関心です。特に統計力学のそもそもの問題意識は、たとえば熱が伝わったり水が流れたりするような「巨視的」現象を、それらはすべて気体や水の「微視的」分子が運動することによって引き起こされるということを示し、何が生じているかを明らかにすることでした。20 世紀末頃からようやくこうした問題を数学的に厳密な意味で取り扱うことができるようになり、流体力学極限と呼ばれています。また、近年では場の理論の一種である共形場理論と呼ばれるものを確率論の枠組みで取り扱うことができるようになりつつあり、大変注目を集めているとともに、活発な研究が行われています。
いずれにせよ、戦時中の伊藤清先生の理論に始まる確率解析は偏微分方程式論・関数解析とともに発展しながら無限次元解析学という形をとり、現在でもまだ、その適用範囲をいわゆる伝統的な数学の枠の外にまで広げながら大いに発展しています。