受験生向け研究紹介
上山 健太
数学科 代数学分野
非可換環の表現論と代数幾何学の結びつき
現在の研究テーマ:非可換代数幾何学に関連する環や圏の研究
私の専門は非可換代数幾何学に関連する環や圏の研究です.特に,「Artin-Schelter Gorenstein代数」と呼ばれる非可換次数付き環や,それに付随する「非可換射影スキーム」と呼ばれる圏に興味を持っており,研究を進めています.
代数幾何学は,いくつか多項式の零点集合が定める幾何およびその一般化を研究する学問ですが,代数的側面では可換環(積の交換法則が成り立つ環)の理論がとても重要な役割を担います.
代数側には非可換環(積の交換法則が成り立たない環)もあるので,代数幾何学的な枠組みを非可換にも拡張・活用できればよいのですが,直接的な方法ではうまくいかないことが多いです.それに対して,どう捉えるのがよいのかを研究するのが非可換代数幾何学という分野だといえます.私は,非可換射影スキームを研究することで,射影代数幾何学における顕著な事実が非可換の世界にどう広がっているかを理解したいと考えています.
代数幾何学は,いくつか多項式の零点集合が定める幾何およびその一般化を研究する学問ですが,代数的側面では可換環(積の交換法則が成り立つ環)の理論がとても重要な役割を担います.
代数側には非可換環(積の交換法則が成り立たない環)もあるので,代数幾何学的な枠組みを非可換にも拡張・活用できればよいのですが,直接的な方法ではうまくいかないことが多いです.それに対して,どう捉えるのがよいのかを研究するのが非可換代数幾何学という分野だといえます.私は,非可換射影スキームを研究することで,射影代数幾何学における顕著な事実が非可換の世界にどう広がっているかを理解したいと考えています.
上の図は射影2次曲面の一例です.非可換な射影2次曲面とはどんなものでしょうか?
Artin-Schelter Gorenstein代数に付随する非可換射影スキームの研究に私が注目している主な理由は,次数付き(極大)Cohen-Macaulay加群の表現論との接点が非常に大きいからです.
次数付きCohen-Macaulay加群の(特に安定圏の)情報を用いて非可換射影スキームの(特に導来圏の)ことが分かることがあります.逆に,非可換射影スキームの研究が進展することで,次数付きCohen-Macaulay加群の結果が得られることもあります.それゆえに,次数付きCohen-Macaulay加群の表現論の研究にも力を注いでいます.特に,導来圏や安定圏などの三角圏を,傾理論を用いたアプローチで考察することは重要だと考えています.
次数付きCohen-Macaulay加群の(特に安定圏の)情報を用いて非可換射影スキームの(特に導来圏の)ことが分かることがあります.逆に,非可換射影スキームの研究が進展することで,次数付きCohen-Macaulay加群の結果が得られることもあります.それゆえに,次数付きCohen-Macaulay加群の表現論の研究にも力を注いでいます.特に,導来圏や安定圏などの三角圏を,傾理論を用いたアプローチで考察することは重要だと考えています.
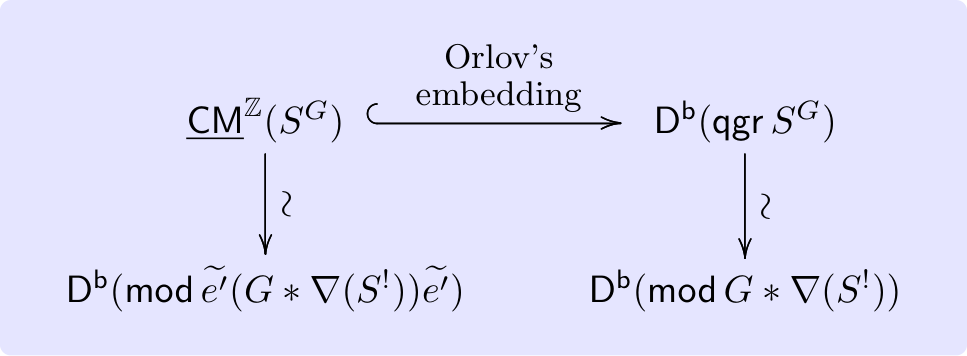
上の図は非可換商特異点に付随する三角圏の様子です.
研究領域:環論,環の表現論,非可換代数幾何学
ここで私が言っている非可換代数幾何学という研究分野は,1990年頃にMichael Artinによって創設されたものです.非可換代数幾何学の発端は,Artin-Schelter (1987) およびArtin-Tate-Van den Bergh (1990) によってなされたある種の3次元非可換正則代数の分類にあります.その正則代数が今ではArtin-Schelter正則代数と呼ばれ,非可換代数幾何学の主要な研究対象となっています.Artin-Schelter Gorenstein代数はArtin-Schelter正則代数を含む環のクラスで,次数付きGorenstein環の非可換類似に対応します.
非可換代数幾何学において,アーベル圏や三角圏(と呼ばれる良い圏)を幾何的なものだと見なして研究することは重要な観点の一つです.例えばArtin-Zhang (1994) は,「射影スキーム上の連接層のなす圏が有限生成次数付き加群の成す圏の商圏と圏同値になる」というSerreの定理や,Gabriel-Rosenbergによるスキームの復元定理に倣い,「非可換次数付き代数に対しても,有限生成次数付き右加群の成す圏のある商圏をその次数付き代数に付随する非可換射影スキームだと見なす」という考えで非可換射影スキームの基礎理論を確立しました.多項式環に付随する射影スキームが射影空間であることから,Artin-Schelter正則代数に付随する非可換射影スキームは非可換射影空間と考えられており,特に盛んに研究されています.とりわけ,有限次元代数の表現論(クイバーの表現論)との関連を研究することは近年の重要なテーマとなっています.
非可換射影スキームは次数付き加群の圏の商圏なので,考察する上で次数付き加群の表現論が欠かせません.中でも,Artin-Schelter Gorenstein代数に付随する非可換射影スキームは,次数付き(極大)Cohen-Macaulay加群の表現論と密接に関係しています.有限次元代数やCohen-Macaulay環を含む環のクラスに整環というものがありますが,整環上のCohen-Macaulay加群の表現論は,可換環論,代数幾何学,表現論が絶妙に絡み合った豊かな研究分野であることが知られています.Artin-Schelter Gorenstein代数は整環とは限らず,それ上の次数付きCohen-Macaulay加群についてはまだまだよく分かっていない状況ではありますが,興味深い理論が展開されていくのではないかと期待しています.
非可換代数幾何学において,アーベル圏や三角圏(と呼ばれる良い圏)を幾何的なものだと見なして研究することは重要な観点の一つです.例えばArtin-Zhang (1994) は,「射影スキーム上の連接層のなす圏が有限生成次数付き加群の成す圏の商圏と圏同値になる」というSerreの定理や,Gabriel-Rosenbergによるスキームの復元定理に倣い,「非可換次数付き代数に対しても,有限生成次数付き右加群の成す圏のある商圏をその次数付き代数に付随する非可換射影スキームだと見なす」という考えで非可換射影スキームの基礎理論を確立しました.多項式環に付随する射影スキームが射影空間であることから,Artin-Schelter正則代数に付随する非可換射影スキームは非可換射影空間と考えられており,特に盛んに研究されています.とりわけ,有限次元代数の表現論(クイバーの表現論)との関連を研究することは近年の重要なテーマとなっています.
非可換射影スキームは次数付き加群の圏の商圏なので,考察する上で次数付き加群の表現論が欠かせません.中でも,Artin-Schelter Gorenstein代数に付随する非可換射影スキームは,次数付き(極大)Cohen-Macaulay加群の表現論と密接に関係しています.有限次元代数やCohen-Macaulay環を含む環のクラスに整環というものがありますが,整環上のCohen-Macaulay加群の表現論は,可換環論,代数幾何学,表現論が絶妙に絡み合った豊かな研究分野であることが知られています.Artin-Schelter Gorenstein代数は整環とは限らず,それ上の次数付きCohen-Macaulay加群についてはまだまだよく分かっていない状況ではありますが,興味深い理論が展開されていくのではないかと期待しています.
