受験生向け研究紹介
玉木 大
数学科 幾何学分野
ホモトピー論の広がり
現在の研究テーマ:高次ループ空間の構造とその応用
私が数学に興味を持ったのは高校生のとき,講談社ブルーパックスの「組み紐の幾何学」(村杉邦男著) という本を読んだのが切っ掛けでした.組み紐とは次の図のような3次元空間の中の図形のことです.
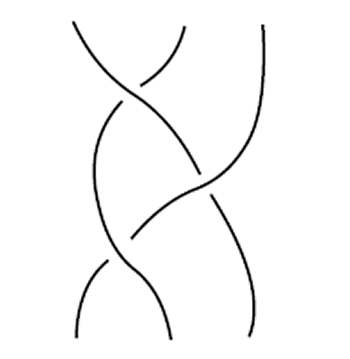
人間の習性(?)としてこのように絡まったものがあるとほどきたくなりますが「紐をほどく」というのは,手を動かせば簡単にできる,そして絵からも直感的に理解できる操作です.しかし,それを数学的にきちんと扱うのにはどうすればよいでしょうか.連続写像という概念を知っていれば,このような「連続変形」を数学的に定義するのは難しくないですが,高校までの数学しか知らなかった私にとっては「紐の変形」のようなものを数学の対象として扱えると知ったのは新鮮な驚きでした.
現代数学には高校数学からは全く想像もできない世界があること,そしてその中でもトポロジーという分野は「紐」のようなかなり毛色の変ったものを扱っているということを知って,大学に入ったらトポロジーを勉強してみたいと思うようになりました.
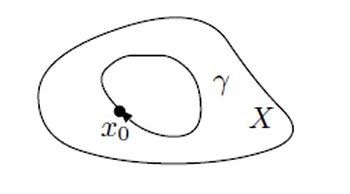
入った大学にもトポロジーの専門家はいましたが,「紐」のような絵に描ける対象ではなく,より抽象的な代数的トポロジーという分野が盛んなところだということが分かり,仕方なくその代数的トポロジーを勉強してみました.勉強してみればそれなりに面白いもので,中でも,多重ループ空間という複雑な構造があることを知り,興味を持ちました.ループ空間とは,ある空間 \(X\) の中の特定の点 \(x_0\) から始まって,同じ \(x_0\) で終わる連続な道 (ループ) 全体のなす空間のことで,普通 \(\Omega X\) という記号で表わします.
現代数学には高校数学からは全く想像もできない世界があること,そしてその中でもトポロジーという分野は「紐」のようなかなり毛色の変ったものを扱っているということを知って,大学に入ったらトポロジーを勉強してみたいと思うようになりました.
入った大学にもトポロジーの専門家はいましたが,「紐」のような絵に描ける対象ではなく,より抽象的な代数的トポロジーという分野が盛んなところだということが分かり,仕方なくその代数的トポロジーを勉強してみました.勉強してみればそれなりに面白いもので,中でも,多重ループ空間という複雑な構造があることを知り,興味を持ちました.ループ空間とは,ある空間 \(X\) の中の特定の点 \(x_0\) から始まって,同じ \(x_0\) で終わる連続な道 (ループ) 全体のなす空間のことで,普通 \(\Omega X\) という記号で表わします.
この,\(X\) から \(\Omega X\) を作るという操作を \(n\) 回繰り返しできる空間を \(\Omega^n X\) と書き \(X\) の \(n\) 重ループ空間と言いますが,\(n=2\) のときが,何と以前聞きかじった組み紐と深い関係にあるらしいことを知ったのは,大学院生になってからでした.組み紐と多重ループ空間の関係は,1970年代から知られていたことなのですが,私にとっては不思議な組み紐との再会でした.更に,留学先のRochester大学での師匠であったFred Cohen教授によって組み紐とループ空間の関係が色々調べられていたのも,また不思議な縁だと思いました.
研究領域:ホモトピー論
組み紐と多重ループ空間の関係を誤解を恐れずに非常に単純化して説明すると,次のようになります:複素平面 \(\mathbb{C}\) の中の \(k\) 個の互いに異なる点の成す空間を\(F(\mathbb{C},k)\) で表わし,\(k\) 点の配位空間と呼びます.この配位空間を全ての \(k\) に関して集め,ある方法で貼り合わせると球面の \(2\) 重ループ空間ができます.そして \(F(\mathbb{C},k)\) という空間におけるループは \(k\) 本の紐から成る組み紐に他なりません.
この配位空間 \(F(\mathbb{C},k)\) は \(x_i=x_j\) という方程式で得られる \(\mathbb{C}^k\) の中の超平面達の補集合と考えることができます.例えば\[
F(\mathbb{C},3)=\left\{(x_1,x_2,x_3)\in \mathbb{C}^3 \ \left| \
\begin{array}{l}
x_1\neq x_2,\\
x_2\neq x_3,\\
x_1\neq x_3
\end{array}\right\}\right.
\]は \(\mathbb{C}^3\) の中の三枚の超平面 \(x_1=x_2\), \(x_2=x_3\), \(x_1=x_3\) の補集合です.このような複数の超平面達の集まりは,様々な分野に登場する基本的な構造で,超平面配置と呼ばれていて,盛んに研究されています.配位空間のような,実数を係数に持つ方程式で定義された超平面を複素数上で考えてできる超平面配置の補集合に対しては,ある方法でSalvetti複体と呼ばれる単体複体(多面体を貼り合せてできる図形)を構成することができるのですが,最近の私の研究での一つの成果は,それが \(2\) 重ループ空間の構造と深い関係にあることが分ったことです.更に\[
x_1+x_2=x_3+x_4
\]などの超平面も追加して考えると,ホモトピー論の重要な課題であるホモトピー群の大域的構造を調べることにも使えるということが分ってきました.
ここで「ホモトピー論」という言葉が出てきましたが,ホモトピー論とは「連続的変形」の数学的な表現であるホモトピーを中心に考えるトポロジーの一分野です.連続的変形にも色々ありますが,これまでに説明した組み紐や多重ループ空間との関連ではoperadという概念が重要です.次の二つの川を考えましょう.
この配位空間 \(F(\mathbb{C},k)\) は \(x_i=x_j\) という方程式で得られる \(\mathbb{C}^k\) の中の超平面達の補集合と考えることができます.例えば\[
F(\mathbb{C},3)=\left\{(x_1,x_2,x_3)\in \mathbb{C}^3 \ \left| \
\begin{array}{l}
x_1\neq x_2,\\
x_2\neq x_3,\\
x_1\neq x_3
\end{array}\right\}\right.
\]は \(\mathbb{C}^3\) の中の三枚の超平面 \(x_1=x_2\), \(x_2=x_3\), \(x_1=x_3\) の補集合です.このような複数の超平面達の集まりは,様々な分野に登場する基本的な構造で,超平面配置と呼ばれていて,盛んに研究されています.配位空間のような,実数を係数に持つ方程式で定義された超平面を複素数上で考えてできる超平面配置の補集合に対しては,ある方法でSalvetti複体と呼ばれる単体複体(多面体を貼り合せてできる図形)を構成することができるのですが,最近の私の研究での一つの成果は,それが \(2\) 重ループ空間の構造と深い関係にあることが分ったことです.更に\[
x_1+x_2=x_3+x_4
\]などの超平面も追加して考えると,ホモトピー論の重要な課題であるホモトピー群の大域的構造を調べることにも使えるということが分ってきました.
ここで「ホモトピー論」という言葉が出てきましたが,ホモトピー論とは「連続的変形」の数学的な表現であるホモトピーを中心に考えるトポロジーの一分野です.連続的変形にも色々ありますが,これまでに説明した組み紐や多重ループ空間との関連ではoperadという概念が重要です.次の二つの川を考えましょう.
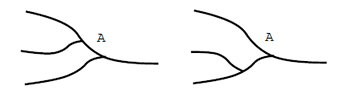
川の中流にあるAという町に住んでいる人にとっては,この二つの流れは全く異なるものです.もし真ん中の支流の上流で大雨が降ったら,左の場合は町Aは洪水になるでしょうが,右の場合は影響を受けません.しかし,最下流では三つの川の流れは一つになってしまうので,途中がどう繋がっていようが関係ありません.3個の実数を掛けるときに成り立つ\[ (a\cdot b)\cdot c = a\cdot (b\cdot c)\]という公式は,最下流に住んでいる人の視点と考えることができます.しかしながら,川の流れのように,最終的な答えだけでなくどこでどのように合流するかが重要になる場合もあるわけです.このように,2個以上のものを合せるときに何種類もの方法がある場合を考えるためにoperadというものが考え出されました.
また,川の例で真ん中の支流の合流地点を「連続的に移動」していくと左の川は右の川になりますが,operadはそのような演算の連続変形に深く関係しています.演算の連続変形が登場する最も典型的な例がループ空間でのループの連結による演算であり,operadはその研究の過程で1970年代に登場したものです.ところが,1990年代以降,様々な幾何学的および代数的構造,更には数理物理学に現われる構造もoperadを用いて記述できることが分かり,数理科学の様々な分野で使われる概念となっています.
他の分野との関連では,もう一つ「モデル圏」という概念も重要です.モデル圏とはホモトピーの概念を抽象化し,「連続的変形」を他の場面でも使えるようにしたものです.例えば
・計算機科学の並列処理の理論
・非可換代数幾何学
・数理論理学
・…
このように大域的な視野に立って,考えている研究対象全体を見渡して考えるという視点は,1940年代にEilenbergとMacLaneにより代数トポロジーのために導入された圏と関手の理論に寄るところが大きく,この分野の最大の特徴と言えるかもしれません.
また,川の例で真ん中の支流の合流地点を「連続的に移動」していくと左の川は右の川になりますが,operadはそのような演算の連続変形に深く関係しています.演算の連続変形が登場する最も典型的な例がループ空間でのループの連結による演算であり,operadはその研究の過程で1970年代に登場したものです.ところが,1990年代以降,様々な幾何学的および代数的構造,更には数理物理学に現われる構造もoperadを用いて記述できることが分かり,数理科学の様々な分野で使われる概念となっています.
他の分野との関連では,もう一つ「モデル圏」という概念も重要です.モデル圏とはホモトピーの概念を抽象化し,「連続的変形」を他の場面でも使えるようにしたものです.例えば
・計算機科学の並列処理の理論
・非可換代数幾何学
・数理論理学
・…
このように大域的な視野に立って,考えている研究対象全体を見渡して考えるという視点は,1940年代にEilenbergとMacLaneにより代数トポロジーのために導入された圏と関手の理論に寄るところが大きく,この分野の最大の特徴と言えるかもしれません.
