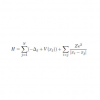Research Theme: Mathematical Fluid Mechanics

I study nonlinear partial differential equations in fluid mechanics, especially, the Navier-Stokes equations and the Euler equations.
The motion of a viscous incompressible fluid in $3$-dimensional domains $\Omega$ is governed by the Navier-Stokes equations:
$$ \mbox{(N-S)} \left\{ \begin{array}{rcl} \partial_t u-\Delta u +u\cdot\nabla u +\nabla p & = &f, \\ \nabla\cdot u & = & 0,\\ u|_{\partial \Omega} & = & 0,\\ u|_{t=0}&=&a, \end{array} \right. $$
where $u=(u^1(x,t), u^2(x,t), u^3(x,t))$ and $p= p(x, t)$ denote the velocity vector and the pressure, respectively, of the fluid at the point $(x, t) \in \Omega \times (0,\infty)$. Here $a$ is a given initial data and $f$ is a given external force.
The motion of an ideal incompressible fluid in $3$-dimensional domains $\Omega$ is governed by the Euler equations:
$$ \mbox{(E)} \left\{ \begin{array}{rcl} \partial_t u +u\cdot\nabla u +\nabla p & = &f, \\ \nabla\cdot u & = & 0,\\ u\cdot \nu|_{\partial \Omega} & = & 0,\\ u|_{t=0}&=&a. \end{array} \right. $$
It is known that if the initial velocity $a$ is small in some sense, then there exists a global-in-time smooth solution to the Navier-Stokes equations. On the other hand, if $a$ is not small, the global existence of smooth solutions remains a famous open problem.
Research Area: Nonlinear Partial Differential Equations
I study nonlinear partial differential equations by using Functional Analysis and Harmonic Analysis. A partial differential equation is an equation involving an unknown function and its partial derivatives. Typical examples are as below.

The Laplace equation: $$ -\Delta U(x)=0, $$ the heat equation: $$ \partial_t T(x,t)-\Delta T(x,t)=0, $$ the wave equation: $$ \partial_t^2 w(x,t)-\Delta w(x,t)=0, $$ the nonlinear Schroedinger equation: $$ \partial_t \psi(x,t)-i\Delta \psi(x,t)=F(\psi,\bar \psi), $$ and the Navier-Stokes equation: \begin{equation*} \left\{\begin{split} &\partial_t u-\Delta u +u\cdot \nabla u +\nabla p = f, \\ &\nabla \cdot u=0 \end{split} \right. \end{equation*}
Since many natural phenomena are described by partial differential equations, the mathematical analysis of partial differential equations plays important roles in many various areas of natural science.