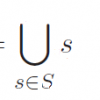Current research theme: divergence theorem in infinite dimensional spaces
Everybody may agree that one of the most influential theorems in the scientific world is the fundamental theorem of calculus. It asserts (in one dimensional case) that the differential and integral are converse each other. It also says that a sum of the values of a function in some domain is a difference of its values at the boundary, so that we can know information inside the domain by that of the boundary only. Gauss' divergence theorem shows that this fact still holds in multi dimensional cases. These relations are one of the most fundamental in analysis, for instance, it is used to extend the concept of functions though there are several such theories. In addition, this type theorems are basis of applied mathematics such as a vector analysis and a foundation of modern geometry. This is often compared to scan a house only by walking around it after putting a suitable function.
However, such situation completely differs in infinite dimensional spaces. For example, we have no natural "volume" to define the integral. To see it, let us consider an infinitesimal small cube (length $1/n$) which has volume $1/n^d$ in the $d$-dimensional space. It has vanishing volume ($d \to \infty$). Also we cannot consider natural "shift" (group action) which fits to the volume-like concept.
But they finally met together in the studies of probability theory in the late of 1970's, and we got a satisfactory differentialintegral calculus in infinite dimensional spaces based on measure theory. This theory is often named after a mathematician who made a breakthrough in this field, the Malliavin calculus. This theory states that it holds a formula of partial integration (which is a general form of the elementary theorem of calculus) but had difficulty for bounded domains to say something
like divergence theorems. It is quite contrastive that we first study for bounded sets and then had difficulty to extend to infinite region in finite dimensional cases. This comes from the fact that, in natural spaces (say, we may consider the "size" of vectors), bounded closed sets are compact which means they behave nicely if and only if the space is finite dimensional, that makes completely difficult to formulate divergence theorems. Although we have had such a theorem for a smooth region like a ball, we want to formulate in a non-smooth region like a rectangle.
Research Area: Stochastic Analysis
When Einstein studied Brownian motion theoretically in the beginning of 20th century, they started to formulate the motion in a mathematical way. It ws to construct a nice map from an interval $[0,1]$ to an infinite dimensional space of the continuous functions using the Fourier analysis and then induce a probability measure on it, which is now called the Wiener measure. Once we succeeded in constructing such a fundamental object like a Brownian motion, it is natural to ask for other diffusion processes to construct in a mathematically rigorous way. But it had been a hard task, and Kolmogorov tried to formulate it as a problem of certain partial differential equations but unfortunately unsatisfied.
In 1942, Kiyosi Itô published a really revolutionary paper "Differential equations determining Markov processes", in which he formulated a theory of integration (Itô integral) based on the path of Brownian motion, having been mystical even now, and defined and formulated the concept of stochastic differential equations, and then showed that if it has a unique solution, then it is a diffusion process. Also a prototype of a fundamental formula (called Itô's formula later) in stochastic calculus which decomposes the Itô process into the Itô integral and the usual Lebesgue integral had already been shown. But in this moment they required some smoothness for coefficients.
Later, the conditions to have solutions are weakened by, among others, Maruyama and Skorokhod in late of 1950's. But to construct diffusion processes, it has not been solved even some analytic studies by Tanaka and Skorokhod in late of 1960's, and then was completely solved by Stroock and Varadhan combining both theories around 1970's. But to clarify the relation with the concept of the Itô uniqueness, we had to wait for the complete study the theory of stochastic differential equations by Yamada and Watanabe in early 1970's.
Diffusion processes actually describe background motions of some differential operators and partial differential equations, which appear after we take "average" of the process, but we do not require such a condition like ellipticity which is often unavoidable in functional analytic methods. This is a really big advantage of stochastic analysis, but unfortunately, it was a long unsolved question that it is possible in a framework of stochastic analysis to show the solution like its average of its distribution
is really differentiable. This was solved by the Malliavin calculus in late of 1970's, and then the theory was completed by Watanabe, Shigekawa, and others. It was applied to such many fields like H\"olmander's hypoellipticity problem and Atiyah--Singer's index theorem, which are monumental achievements of stochastic analysis.
But we should note that we may apply the Malliavin calculus to the solutions of the stochastic differential equations only when they have strong solutions, in other words, the solutions can be reconstructed from the source of randomness. When an equation has a non-strong (weak) solution which was first discovered by Tanaka, namely, the randomness of the solution is over those of the source of randomness, we could not. Although it is known these difference disappear in the structure of partial differential equations, it is serious in the probability theory. These two concept are also important to construct market models in mathematical finance, and also pointed out that has deep relation with the theory of operator algebra from the concept of noise introduced by Tsirelson recently.
On the other hand, we regard the theory of stochastic analysis including the Itô calculus and the Malliavin calculus are completed, and we are mainly interested in such concrete problems like mathematical finance and mathematical physics like rigorous statistical mechanics and quantum field theory. Especially, a big problem in statistical mechanics is to show macroscopic phenomena like heat conduction or water current are caused from microscopic motions of molecules of gases or waters. It was just at the end of 20th century that we can handle these problems mathematically rigorously, which we call the hydrodynamic limit.
Anyway, the stochastic analysis started from a paper of Itô during the second world war has been growing together with partial differential equations and functional analysis, and now forms a shape of infinite dimensional analysis, and is still expanding to outside of classical field of mathematics.