Present research theme: elementary particle physics, mathematical physics
My research fields are elementary particle physics and mathematical physics. The unfamiliar word "symmetry" appears in the title, and let's start with that explanation. Symmetry is one of the fundamental ideas of modern physics. When we apply certain operation on the object we are thinking about (we call it a system), if that object does not change (we say it is invariant), that operation is called symmetry operation and we say that this system has symmetry. For example, if an equilateral triangle plate rotates 120 degrees around the center, it returns to the same state as the original, so it has rotational symmetry of 120 degrees. The study of physics is to observe natural phenomena closely, to explore the laws in it, to make a theory, and to explain natural phenomena using that theory. Various physical laws were examined, and various symmetries were found. Everyone in high school students will surely know the law of conservation of energy and the law of conservation of momentum. These are due to the symmetry of uniformity of time and uniformity of space. There is another law called the law of conservation of angular momentum, and it is due to the symmetry of space isotropy.
Attempts to reverse the flow of "natural phenomena → physical law (= theory) → symmetry", and to "make a theory to have certain symmetry" (and apply it to natural phenomena) began to be done. Everyone would have heard of Einstein's theory of relativity. Einstein created the theory of special relativity by requiring symmetry under the Lorentz transformation and the principle of invariant light speed. This was a revolutionary theory that transformed the concept of time and space completely. Einstein further constructed a theory of gravity, the theory of general relativity, by requiring symmetry under general coordinate transformation and equivalence principle. The theory describing elementary particle physics is the gauge theory obtained by requiring symmetry under gauge transformation. In this way, symmetry can be used as the guiding principle in theory construction.
Particles that can not be divided further finely are called elementary particles, and the study to investigate elementary particles and the force acting therebetween (force is mediated by exchanging particles, so the force is called interaction) is elementary particle physics. Four fundamental forces of nature are known: electromagnetic interaction which is electric and magnetic force, weak interaction related to nuclear decay, strong interaction related to nuclear force, gravitational interaction of universal gravitation. Three interactions other than gravity are described by gauge theory with gauge symmetry on the framework of quantum field theory. Electromagnetic interactions and weak interactions are unified and become electroweak interaction, and its predictions match well with experiments. The classical theory of gravity is completed as the theory of general relativity, but its quantum theory has not been completed yet. The most promising candidate for the quantum theory of gravity is string theory which regards elementary particles as strings extending one dimensionally rather than point particles. Superstring theory with symmetry named supersymmetry is the ultimate unified theory (the most promising candidate) that includes quantum theory of gravity and unifies all elementary particles that form substances and elementary particles that mediate forces. It is known that not only the strings extending one dimensionally but also Dp-branes extending to space p dimensions are equally important.
When a point particle moves, a line (called a world line) is formed. Likewise, when the string moves, a surface (called a worldsheet) is formed. Considering string theory as a field theory on this worldsheet, it is a conformal field theory. Conformal field theory is the quantum field theory with symmetry under conformal transformation (which may change length, but does not change angle). The symmetry of the conformal field theory in two dimensional spacetime is expressed by an infinite dimensional algebra called Virasoro algebra, and its representation theory has been investigated in detail. One of the advantages of the discussion of symmetry is that we can argue the universal nature not depending on the details of the system by using representation theory of groups and algebras expressing symmetry. If symmetry is large, it will be possible to discuss strongly.
I wanted to understand physics from the viewpoint of symmetry, I focused on research on infinite dimensional algebra such as Virasoro algebra, which express symmetry, and research on various exactly solvable models etc. Rather than being directly involved in natural phenomena, it is a research focused on mathematical aspects in physics theory and is called mathematical physics. Since we need various mathematics, I will not go into details of research, but I will introduce one method that I prefer. It is a free field realization, and it is a method of realizing complicated objects using well-understood things (free fields). For example, the embedding pattern of degenerate representation of Virasoro algebra is given as shown in
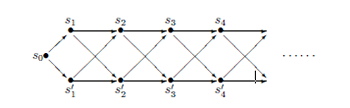
In free field realization, from the Fock space of free fields with simple structure, by considering the complex as shown in
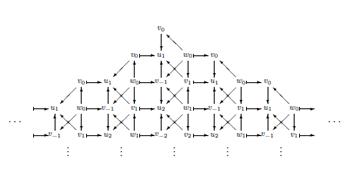
the irreducible representation space of Virasoro algebra, which we want, are extracted by using cohomology method. Also, the exactly solvable lattice model in two dimensional space is a statistical model given Boltzmann weight satisfying the Yang-Baxter equation for each square in the figure
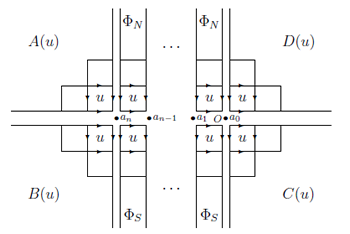
By expressing the corner transfer matrices (\(A,B,C,D\)) and the type I vertex operators (\(\Phi_N,\Phi_S\)) in terms of free fields, we can calculate the correlation functions by taking their traces on the Fock space.
Recently I am doing research on exactly solvable quantum mechanical models, and interesting results are obtained about a new type of orthogonal polynomial.
Message to high school students
I was interested in elementary particle physics for the first time as a junior high school student. When I saw scientific magazines and others, I felt longing for the mysterious world of the theory of special relativity and the microscopic world of elementary particles such as quarks. When I became a high school student, I had a physics lesson and I was interested in being able to investigate natural phenomena according to the laws of physics and by using mathematical expressions. I thought that I would like to major in physics, which is the foundation of natural science, especially elementary particle physics dealing with objects of the smallest unit, and I went to university. I would like you to find a topic that you can come interested in by all means.Even a small topic or a big topic is fine. If you find something, please learn about it on your own. In study at school until a high school, the scope of study may have been limited, but learning is free. If you have an interesting topic, you can go anywhere. Even at high school, the academics that you first learn after entering university are not spectacular topics, but many plain sorts of things that you say even as a basic physical strength creation. However, once you acquire this basic physical strength, you will be able to understand spectacular topics for the first time, so I would like you to devote yourself to studying while keeping the feelings of your admiration when entering university.