Research Area: Algebraic Topology
My research field (from a global point of view): Topology is in the realm of geometry and it deals with more abstract and general figures in the study. The two-dimensional sphere, which is a kind of manifolds (beautiful figures), is a geometrical object. One might be concerned with the shape and bend. However, in topology, even the dimension collapses if the sphere has a hole. Two spaces are called homotopy equivalent if one can be deformed continuously to another. For example, the real line is homotopy equivalent to the set of singleton and the circle is not crushed in the sense of topology. While the definitive aim of topology is to classify spaces under homotopy equivalence, it is fairly difficult to make it in general. As good news for the purpose, we can use effective homotopy/topological invariants, namely, homotopy groups, (co)homology groups and those endowed with more additional structures. The invariants convert geometrical information to algebraic one. Thus one can know the difference between given two spaces if values of their homotopy invariants are distinguished in the framework of algebra.
General tools/concepts for the study: In order to consider the invariants uniformly, and to compare them, we appeal to category theory. The theory was invented by S. Eilenberg and S. Mac Lane in the early 1940s. It builds many bridges between topology and algebra. A category consists of objects which we deal with, and morphisms, each of which is an arrow form an object to another. Roughly speaking, in a category, objects and morphisms are regarded as words and grammar, respectively. In order to understand different languages, we need to translate words and sentences. Such a translator is called a functor between two categories. A natural transformation which connects two functors is also one of important concepts in category theory. These notions are displayed as follows with categories \(C\) and \(D\).
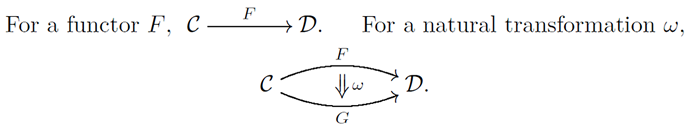
Devises, tools and concepts such as functors and natural transformations are widely applicable to mathematical sciences. (For example, the program language Haskell respects categorical manners in the construction.) I suppose that category theory waits for its aggressive application to science and technology.
Going back to my research, various invariants mentioned above are indeed functors. Natural transformations assume the comparison of invariants. Thus category theory does work well in topology and algebra since the abstract theory have been coined aiming its applications to different research fields under a common language.
Research subjects: I) String topology: My recent work concerns string topology in which one obtains interesting algebraic structures on the homology groups of the free loop spaces of manifolds and related spaces. The $(1+1)$-dimensional topological quantum field theory structure, which appears in a functor category with the cobordism category of circles as the domain, enriches the homology and then string topology. With collaborators, I have given explicit formulae for string operations.
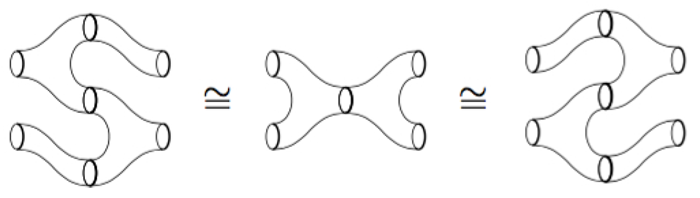
Equivalences in the cobordism category
II) Schemoids: An association scheme (AS) captures combinatorial structure for a partition of the cartesian product of a set with itself. The notion plays a crucial role in algebraic combinatorics, including the study of designs and graphs, and in coding theory. We have been interested in developing such a combinatorial object in the framework of category theory. Then the notion of a schemoid has been proposed by the author with his collaborators as a generalization of ASs from a small categorical point of view. We apply aggressively representation theory of algebras, homotopy theory of small categories and topos in the study of schemoids.
III) Diffeology: Diffeological spaces are comparatively new research objects introduced by J.-M. Souriau in the early 1980s. The notion has strongly inspired me. In fact, the category $\mathsf{Diff}$ of diffeological spaces allows us to investigate simultaneously manifolds and their function spaces in the notion without introducing more complicated structures. A new project in my research has started with diffeology.
This essay is concluded with my favorite diagram consisting of categories and functors. The diagram below explains that the category $\mathsf{Diff}$ is connected to other four categories with very exiting functors. Thus $\mathsf{Diff}$ is suited in a strategically important location of our study.
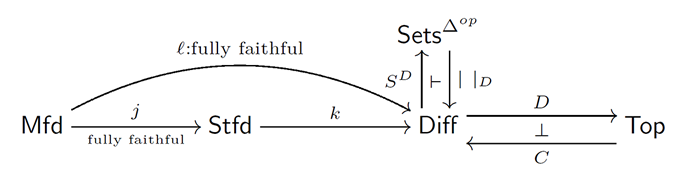
Here $\mathsf{Mfd}$, $ \mathsf{Stfd}$, $\mathsf{Sets}^{\Delta^{op}}$ and $\mathsf{Top}$ denote the categories of manifolds, stratifolds, simplicial sets and topological spaces, respectively. Adding the category of algebras, these categories will expand further diffeological worldview.
I hope that you enjoy and study diffeology from geometrical, topological, algebraic and categorical points of view with us.