現在の研究テーマ:空間の代数的模型
集合に近さ、遠さ、あるいは広がり、繋がりの概念を定義したものが「位相空間」(以下空間) と呼ばれる幾何学的な対象で、集合に演算を定義したものが「群」「環」と呼ばれる代数的な対象です。私は空間を代数的な対象で近似し、それを用いて元の空間を解析することに興味を持ち研究を続けています。その精神はちょうど、平面図形を座標平面に埋め込んで方程式により記述し、方程式を解析することで元の図形の性質を考察する(皆さんの学ぶ(学んだ)) 座標幾何学に通じるものがあります。最近は、特に2つの空間の間の写像全体がつくる「写像空間」を代数的な対象に変換して研究しています。この研究ついて以下説明します。
空間の点にもう一つの空間の点を対応させることで「写像」という概念が生まれます。私の専門分野であるトポロジーにおいては、ある空間を考察するとき、より基本的な別の空間を取りその2つの空間の間の写像全体を調べることで、もとの空間を考察する方法を用います。基本的な空間として球面を選び、写像全体の集合に群構造を入れたものがホモトピー群で、この群の研究が代数的トポロジーの出発点であるといえます。さて変換についてですか、まず空間のつくる圏(後述)から代数的な対象がつくる圏への適切な関手(後述)を用いて、写像空間を代数化します。ここで現れる対象が空間の代数的模型と呼ばれるもので、関手によっては空間の特性をそのまま引き継ぐもの(でも複雑)、空間の多くの情報は消えてしまうけれど扱いやすいもの、と様々な形を持ちます。ここで最近の研究から具体例を使って考察方法を大雑把に説明しましょう。
例えば写像空間のホモトピー群のある重要な部分群\(G_n({\mathcal F}(U, X; f))\)を調べようと思うならば群のつくる圏で次の「図式」を考えます。
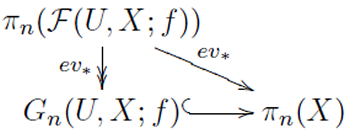
図式とは対象の性質を記述している、例えば基盤の電子回路図のようなものです。次にこの図式を可換化します。そして双対を考え、ベクトル空間の圏に対象を写せば、図式
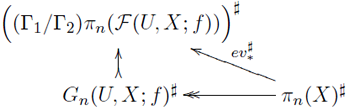
を手に入れることが出来ます。これをさらに適切な関手で可換微分代数のつくる圏に写し、そこで写像空間の代数的模型を熟考することでに次の図式が得られます。
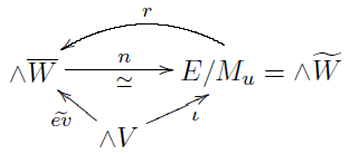
これを"じっと見て"考察することで、\(G_n({\mathcal F}(U, X; f))\)の形がわかり、写像空間の性質も見えてきます。
研究領域:幾何学 代数的トポロジー
平面は一点と「同じ」といったら驚くでしょうか? 平面には座標が定義でき様々な関数のグラフもかけますが、一点の上で出来ることはほとんどありません。ところがトポロジーと呼ばれる幾何学の上では平面も3次元の空間も一点と同じになってしまいます。これらの空間はすべて一点に「縮め」ることが出来るから「同じ」なのです。円は穴が開いていて、自分自身の中で一点に縮めることが出来ません。ですから円は先の3つの空間、点、平面、3次元空間とは同じではありません。長さや体積、面積が変わっても「同じ」とみなすトポロジーにおいては残念ながら微分積分のみで空間を解析することは非常に難しく、その上で微分が出来ない空間を扱うこともあります(私の研究対象のほとんどがこのような空間です)。そこでこうした幾何学的な対象を考察するために、足し算や掛け算といった演算が出来る「群」「環」などの代数的な世界に空間を連れて行って、演算を用いてまたは数を比較して空間を解析する方法を用います。
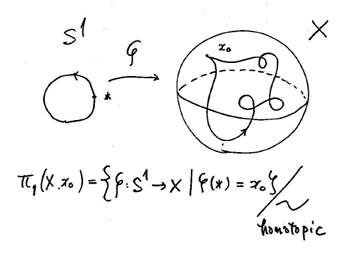
もう少し数学的な用語を交えて説明しましょう。まず"対象"と呼ばれるものと、対象が2つ順に決まると定まる"射"の集合達からなる世界を「圏」と呼びます。ちょうど集合達が対象となり、集合\(A\),\(B\)が2つ定まると\(A\)の元に\(B\)のある元を対応させる写像(関数)を射として集合の圏が現れます。さらに圏どおしを繋ぐものを「関手」と呼んでいます。幾何学的対象のつくる圏から代数的な圏への関手であり、上に述べたようなトポロジー的性質が同じ空間を同じところへ写すものは特に重要で「位相不変量」と呼ばれています。
現在までに空間を分類するために多くの位相不変量が定義され、トポロジー研究に応用されています。その代表的な関手(位相不変量)である基本群を簡単に説明しましょう。まず空間\(X\)とその上の点\(x_0\)を一つとります。そして円\(S^1\)から\(X\)への写像全体を考えます。ただし円の指定された一点は常に基点\(x_0\)に写されるとします。こうして空間上に\(x_0\)を出発してまた\(x_0\)に戻ってくるたくさんの閉じた道を考えたことになります。2つの道がその空間\(X\)上で連続的に変形して一致する場合、それらの道は「ホモトピック」とよばれ、この関係で道全体を類別したものを\(\pi_1(X, x_0)\)(上図参照)と表します。2つの道を基点\(x_0\)で繋げると1つの道が出来ます。2つの"もの"に1つの"もの"を対応させる「演算」が定義できました。こうして得られた群が空間\(X\)の基本群です。またさらに円を高次元の球面(絵にはかけないけれど)にして同様の構成を行うと先に述べたホモトピー群が得られます。
こうした位相不変量やそれらを計算する道具や方法は、トポロジー研究を豊かにしているばかりではなく、数学の他分野に輸出され応用されているという事実もここで付け加えおきます。
前頁で説明した私たちの研究世界をさらに大局的な見地から眺めてまとめとします。2つの圏\(\mathcal{C}\)と\(\mathcal{D}\)を考えます。どちらも射の変形が可能で先の話題にも出てきた「ホモトピック」という関係が定義できる圏とします。このとき2つの対象の間の射がつくる集合においてホモトピーで変形して重なるものを同一視して出来る圏、ホモトピー圏を考えることが出来ます。さらに圏を行き来することを可能にする関手\(F\)と\(G\)が存在したと仮定します。

私たちがこうした状況に期待することは、上の関手がそれぞれのホモトピー圏の間に関手を誘導し2つのホモトピー圏が同値になるということです。

このとき例えば幾何学を代数的に考察することが可能になり、また逆も真となります。どのような圏を考えるのか、良い性質を持った関手\(F\)や\(G\)は何か、そこから幾何学的対象のまたは代数的対象の何が探れるのか、考えることはまだまだたくさんあります。