現在の研究テーマ:埋め込み
図形の性質を調べる分野が幾何学です.私の研究は「位相幾何学」という幾何学の一分野に属します.中でも「多様体」というタイプの図形に興味があります.この文章に出てくる図形は全て多様体です.
多様体論において長年の懸案だったPoincaré(ポアンカレ)予想はG.Perelmanにより解決されました.2006年の国際数学者会議においてFields賞の授与が決定されたもののPerelman本人が受賞を辞退したこともあって,当時かなりセンセーショナルに伝えられたことは(本文執筆時点では)記憶に新しいところです.NHKでもPoincaré予想に関する特集が組まれ,その中で3次元やら4次元やらの空間が...という話が出てきたときに,3次元はともかく,いったい4次元とは何だろう,と考え始めてしまい,夜も寝られなくなった方はおられないでしょうか.そんな中高生の皆さんには(社会人の方も),ぜひ信大理学部で数学を勉強してほしいと思います.
しかし,こうしたきっかけで大学の数学を勉強し始めても,実際にPoincaré予想のような問題の意味をつかめるようになるのは,そう簡単ではないのも事実です.本屋で適当な教科書を手に取ってみられると,その多くは数式や矢印を無味乾燥に並べているだけに見えます.例えば前述の4次元空間も,簡単に言ってしまえば,4つの実数の組全体のなす集合
\[\mathbb{R}^4=\{(x_1,x_2,x_3,x_4)\mid x_i\,\text{は実数}\}\]
であり,これではドラえもんのポケットに詰まっているはずの夢や希望は全く見えてきません.決して大学の数学に夢や希望がないわけではなく,誰にでも平等に同じ内容を伝えるために主観を排して書かれているのであって,順を追って頑張って勉強すれば,誰にでも無味乾燥でない4次元空間の姿が見えるはずなのですが,「頑張って」というところが大変なわけです.私自身も4次元(や,高次元)の姿が見えたとはちっとも思えません.以下では,高次元の姿を見ようとした/している人々の悪戦苦闘の様子を,ほんの一部だけお話してみたいと思います.強調しておきたいのは,大変だからこそ面白い,ということです.
私の研究は,多様体(図形)の埋め込みに関係します.埋め込みとは,3次元や4次元,あるいは一般に\(n\)次元の多様体を,それよりもっと高い次元の空間内に実現することで,図形を「見る」ための手段の一つです.具体例を考えてみましょう.お手元に紙があれば,同じ大きさの円板を二つ切り取ってください.それらをふちに沿ってテープで貼り合わせると,(少しシワの寄った)紙製ピンポン玉ができます.これを球面と呼び,\(S^2\)という記号で表します.平面的な紙を使って作れたので,\(S^2\)は2次元の図形です.2次元の図形\(S^2\)が,我々の住んでいる3次元空間に実現されたわけです.これは\(S^2\)の3次元空間への埋め込みの一例です.
研究領域:埋め込み全体の様相
地球の表面だけを見て,中身を考えなければ,だいたい\(S^2\)です.\(S^2\)上に住んでいる我々は,ふつうは地面が丸いなどとは夢にも思わず,足元に見える平らな地面がどこまでも続いている,と考えることでしょう.丸いことを知るには,地球からちょっと離れて,実際に「見る」のが手っ取り早い方法です.つまり,宇宙空間という3次元空間に地球\(S^2\)が入っている(埋め込まれている)ことにより,我々は\(S^2\)の本当の姿を「見る」ことができます.
もう少し込み入った例を考えます.お手元に紙があれば,\(2\rm{cm}\times 15.7\rm{cm}\)くらいの帯を一つ作り,一度ひねって細いほうの端を貼り合わせてください.有名なMöbius(メビウス)の環ができます.そのふちを辿ってみると,ひとつながりになっていることがわかります(長さは\(31.4\rm{cm}\)ですね).別に直径10cmの円板を作り,そのふちとMöbiusの環のふちを貼り合わせてみてください(下図参照).
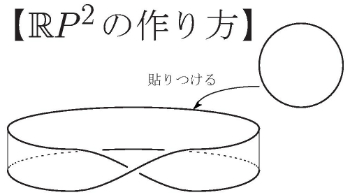
できてしまった方はおられますか?そんな方は何かの才能があるかもしれません.こうしてできるはずの図形(射影平面という名前がついていて,\(\mathbb{R}P^2\)という記号で書かれます)は実は,決して3次元空間に埋め込まれないことが知られています.さきほどの紙製ピンポン玉\(S^2\)も\(\mathbb{R}P^2\)も,紙からできる以上は同じ2次元の図形です.しかし\(S^2\)は3次元空間に埋め込めるのに,\(\mathbb{R}P^2\)は無理なのです.同じ2次元の図形でも,\(S^2\)と\(\mathbb{R}P^2\)の違う姿が,埋め込みの可否という性質に現れているということです.
さきほど紙での作製を試みていただいた\(\mathbb{R}P^2\)ですが,工夫次第で何となく作れた方もおられるかもしれません.実は\(\mathbb{R}P^2\)は,「自分と交わって良ければ」3次元空間に実現できることが知られています.これをはめ込みと言います.下図はW.Boyという人が考案した,\(\mathbb{R}P^2\)の3次元空間へのはめ込みです.自分と交わっているので若干見づらいかもしれませんが,なんだかよくわからなかった\(\mathbb{R}P^2\)の姿が少し垣間見えないでしょうか.

埋め込みのことを紹介するのに欠かせないのが絡み目です.次の図のように,輪になったヒモが3次元内で絡まったものが絡み目です.これは輪っかの3次元空間への埋め込みです.
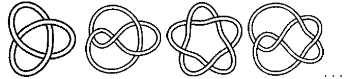
絡まり方がいろいろあるのは,輪っかよりはむしろ3次元空間のほうの性質を反映しています.我々は3次元空間に住んでいますから,3次元の図形のことはよくわかりそうなものですが,実は全くそうではありません.例えば先述のPoincaré予想は,\(S^2\)の「3次元版」である\(S^3\)の特徴づけに関する問題です.\(S^2\)と同じように,\(S^3\)も3次元の中では基本的なもののはずですが,Poincaré予想の解決には100年ほどを要しました(高次元に拡張された問題のほうが先に解かれてしまいました).それくらいに3次元の図形は難しいのですが,実はその難しさは絡み目に集約されているのです:
定理(W.B.R.Lickorish, A.H.Wallace).3次元の図形の分類は,絡み目の分類と「ほぼ」等価である.
絡み目理論は非常に盛んに研究されていますが,その背景にはこの事実があります.我々が住む宇宙も3次元ですから,絡み目,埋め込みは宇宙の形を教えてくれる,かもしれません.
絡み目がそうであるように,一つの図形がいろいろな埋め込み方を許容する,ということはしばしばあり得ます.例えば紙製ピンポン玉\(S^2\)は,3次元空間への埋め込み方は本質的に一通りですが,実は4次元空間への埋め込み方(2次元絡み目と呼びます)は多種多様です.その分類は4次元空間の性質に関わる重要な問題で,現在も活発に研究されています.
私の研究を大雑把に述べると,多様体(図形)を一つ決めて,その図形が許容する多種多様な埋め込みを全て一斉に考え,その様相を調べる,といったものです.実は6次元などの高次元への埋め込みの様相は非常に整っており,しかし深い構造も含んでいる,といったことが徐々に見えてきています.
※Boy曲面と絡み目の絵は,それぞれ"sketches of topology", "knot atlas"というウェブサイトから拝借しました.