現在の研究テーマ:素粒子理論,数理物理学
私の専門は素粒子物理学・数理物理学です。タイトルに「対称性」という耳慣れない言葉が現れてい ますが,その説明から始めましょう。対称性は現代物理学の基礎的考え方の1つになっています。考えている対象(系と言います) にある操作を施した時に,その対象が変わらない場合(不変と言います),その操作を対称操作と言い,この系には対称性があると言います。例えば,正三角形の板は中心の回りに120度回転すると元と同じ状態に戻るので,120度の回転対称性があります。物理学という学問は,自然現象をよく観察し,その中に潜む法則を探り出して理論を作り,その理論を用いて自然現象を説明する,という事を行うものです。様々な物理法則を調べていき,色々な対称性が見つけられました。高校生の皆さんもエネルギ-保存則や運動量保存則を知っているでしょう。これらは時間の一様性と空間の一様性という対称性に起因するものです。もう一つ角運動量保存則というものがあるのですが,それは空間の等方性という対称性に起因します。
「自然現象→物理法則(=理論)→対称性」という流れを逆転して,「ある対称性を持つ様に理論を作ってみよ」(そしてそれを自然現象に適用してみよ)という試みが行われる様になりました。皆さんはアインシュタインの相対性理論という名前を聞いた事があるでしょう。アインシュタインは,ロ-レンツ変換 の下での対称性と光速度不変の原理を要請する事で特殊相対理論を作り出しました。これは時間と空間の概念を一変する革命的な理論でした。アインシュタインは更に,一般座標変換の下での対称性と等価原理を要請して一般相対性理論という重力の理論を構築しています。素粒子物理を記述する理論は,ゲ-ジ変換の下での対称性を要請して得られるゲ-ジ理論というものです。この様に対称性は理論構築の際の指導原理として用いる事ができます。
それ以上細かく分割できない粒子を素粒子と言い,素粒子及びその間に働く力(粒子をやりとりする事で力が伝わるので力の事を相互作用と言います)を調べる学問が,素粒子物理学です。自然界の基本的な力は,電気や磁気の力である電磁相互作用,原子核崩壊に関係する弱い相互作用,核力に関係する強い相互作用,万有引力の重力相互作用の4つが知られています。重力以外の3つの相互作用は,場の量子論という枠組の上で,ゲ-ジ対称性を持つゲ-ジ理論で記述されます。電磁相互作用と弱い相互作用は統一されて電弱相互作用となり,その予言は実験とよく合っています。重力の古典論は一般相対性理論として完成しているのですが,その量子論は未だできあがっていません。重力の量子論の最有力候補は,素粒子を点粒子ではなくて1次元的に拡がったひもと見なす弦理論です。超対称性という対称性を持つ超弦理論は,重力の量子論を含み,物質を形作る素粒子と力を媒介する素粒子を全て統一する,究極の統一理論(の最有力候補) です。1次元的に拡がったひもだけではなくて,空間p 次元に拡がったDpブレインというものも同様に重要である事が分かっています。
点粒子が動くと線(世界線と言います)ができるのと同様に,ひもが動くと面(世界面と言います)がで きます。弦理論をこの世界面上の場の理論と見なすと,共形場理論になっています。共形場理論とは,共 形変換(長さを変えるかも知れないが角度を変えない変換です) の下での対称性を持つ場の量子論です。2 次元時空での共形場理論の対称性は,ビラソロ代数という無限次元代数で表され,その表現論は詳しく調べられています。対称性の議論の利点の1つは,対称性を表す群や代数の表現論を用いる事により,系の詳細に依らない普遍的な性質を議論できる点で,対称性が大きいと強い議論ができる事になります。
私は物理を対称性の観点から理解したいと思い,ビラソロ代数などの対称性を表す無限次元代数の研究や様々な可解模型などの研究を中心に行って来ました。自然現象に直接関わると言うよりも,物理学の 理論においてその数学的側面に力点を置いた研究であり,数理物理学と呼ばれます。様々な数学が必要となるので研究の詳細には立ち入れませんが,私が好んで用いる手法を1つ紹介しておきます。それは自由場表示というもので,複雑な対象を性質のよく分かったもの(自由場) を用いて表示する方法です。例えば,ビラソロ代数の縮退表現の埋め込みパターンは
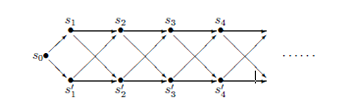
で与えられますが,自由場表示では単純な構造の自由場のフォック空間から,
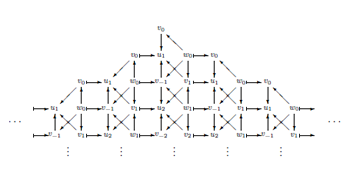
の様な複体を考え,コホモコジーという手法を用いて,求めたいビラソロ代数の既約表現空間を取り出 します。また,2 次元空間での可解格子模型は,
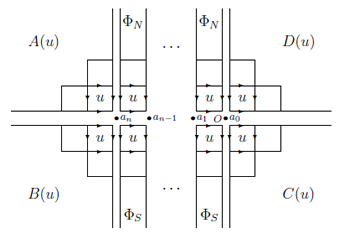
の様に図の正方形1つ1つにヤン・バクスター方程式を満たすボルツマン重みが与えられている統計模型ですが,角転送行列(\(A,B,C,D\))とタイプIの頂点演算子(\(\Phi_N,\Phi_S\))を自由場を用いて表示して,フォック空間上のトレースを取る事により相関関数を計算する事ができます。
最近は解ける量子力学模型の研究を行っており,新しいタイプの直交多項式などに関して興味深い結果が得られています。
高校生の皆さんへのメッセージ
私が素粒子物理学というものに初めて関心を持ったのは中学生の頃で,科学雑誌などを見て特殊相対性理論の不思議な世界やクォ-クなどの素粒子の極微の世界に憧れを感じました。高校生になると物理学の授業があり,自然現象が物理法則に従って起こる事や数式を用いてそれを調べる事ができる事に興味を覚え,自然科学の基礎となる物理学を,中でも最小単位の物体を扱う素粒子物理学を専攻したいと思い,大学に進学しました。皆さんにも是非何か興味を持てる話題を見つけてもらいたいと思います。小さな話題でも大きな話題でも構いませんから何か見つけたら,それについて自ら進んで学んでみて下さい。高校までの学校の勉強では,やる範囲はここまでという枠がはめられていたかも知れませんが,学問というものは自由なのです。興味を持った話題があればどこまでも進んで行って良いのです。高校でもそうでしょうが大学に入学して先ず学ぶ学問は華々しい話題ではなくて基礎体力作りとでも言う様な地味なものが多いです。しかし,この基礎体力を身に付けて初めて華々しい話題を理解できる様になるので,大学に入学した暁には憧れの気持ちを持ち続けて勉学に打ち込んで行ってもらいたいものです。