- HOME
- バーチャルオープンラボ
- プラズマ流体の数学解析
〜Macro・Micro両視点からのアプローチ〜
プラズマ流体の数学解析
〜Macro・Micro両視点からのアプローチ〜

研究集会「 International Workshop on Multiphase Flows:Analysis, Modelling and Numerics 」(2022年12月、早稲田大学)での研究発表の様子
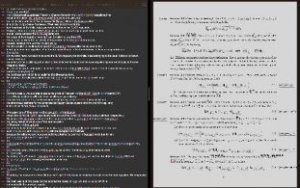
量子修正Hall-MHD方程式の学術論文作成風景
私が修士課程在学中の頃から力を入れて取り組んでいるのは、磁気流体方程式(MHD方程式とも呼ばれる)やHall効果を伴うプラズマ流の数学解析であり、その特徴として、偏微分方程式を代表する放物性・双曲性・分散性など様々な性質が混合した形で方程式の解に影響を及ぼすことが、これまでの研究で明らかになりました。プラズマ流体の研究は太陽フレア発生のメカニズムの解明や核融合炉の制御など応用が広く、これらのある種特異な物理現象を数式を用いて厳密に解明したいという興味のもと、日夜研究に取り組んでいます。
研究から広がる未来
私が研究しているMHD近似やHall-MHD方程式の安定性解析は、核融合炉制御シミュレーションのモデルとして、プラズマ流体モデルは妥当であるかという問いへの回答を与える為、これからの核融合研究の発展に大きく寄与すると考えています。
卒業後の未来像
信州大学工学部で数学を学ぶメリットとしては、工学・物理への応用を意識した、実用的な数学を学べることであると考えています。卒業後はここで学んだ数学を活かし、企業や研究機関などで活躍できる人材の育成を目指しています。





